以上就是给各位分享Android日常学习:OpenGL实践之贝塞尔曲线绘制,其中也会对opengl贝塞尔曲面进行解释,同时本文还将给你拓展AndroidFlutter利用贝塞尔曲线画一个小海豚、And
以上就是给各位分享Android日常学习:OpenGL 实践之贝塞尔曲线绘制,其中也会对opengl贝塞尔曲面进行解释,同时本文还将给你拓展Android Flutter利用贝塞尔曲线画一个小海豚、Android Path绘制贝塞尔曲线实现QQ拖拽泡泡、Android 之二阶贝塞尔曲线的波浪头像 (三阶的爱心飞出)、Android 贝塞尔曲线 折线图等相关知识,如果能碰巧解决你现在面临的问题,别忘了关注本站,现在开始吧!
本文目录一览:- Android日常学习:OpenGL 实践之贝塞尔曲线绘制(opengl贝塞尔曲面)
- Android Flutter利用贝塞尔曲线画一个小海豚
- Android Path绘制贝塞尔曲线实现QQ拖拽泡泡
- Android 之二阶贝塞尔曲线的波浪头像 (三阶的爱心飞出)
- Android 贝塞尔曲线 折线图

Android日常学习:OpenGL 实践之贝塞尔曲线绘制(opengl贝塞尔曲面)
说到贝塞尔曲线,大家肯定都不陌生,网上有很多关于介绍和理解贝塞尔曲线的优秀文章和动态图。
以下两个是比较经典的动图了。
二阶贝塞尔曲线:

三阶贝塞尔曲线:

由于在工作中经常要和贝塞尔曲线打交道,所以简单说一下自己的理解:
现在假设我们要在坐标系中绘制一条直线,直线的方程很简单,就是 y=x ,很容易得到下图:

现在我们限制一下 x 的取值范围为 0~1 的闭区间,那么可以得出 y 的取值范围也是 0~1。
而在 0~1 的区间范围内,x 能取的数有多少个呢?答案当然是无数个了。

同理,y 的取值个数也是有无数个。每一个 x 都有唯一的 y 与之对应,一个 (x,y) 在坐标系上就是一个点。
所以最终得到的 0~1 区间的线段,实际上是由无数的点组成的。
那么这条线段有多长呢?长度是由 x 的取值范围来决定的,若 x 的取值为 0~2,那么线段就长了一倍。
另外,如果 x 的取值范围不是无数个,而是以 0.05 的间距从 0 到 1 之间递增,那么得到的就是一串点了。
由于 点 是一个理想状态下的描述,在数学上点是没有宽高、没有面积的。
但是,如果你在草稿纸上绘制一个点,不管你用到是铅笔、毛笔、水笔还是画笔,一个点总是要占面积的。
毛笔画一个点的面积可能需要铅笔画几十个点了。
在实际生活中,如果要以 0.05 的间距在第一幅坐标系图中画出 x 在 0~1 区间的一串点,最终结果就和直接画一条线段没啥差别了。
这就是现实和理想的差别了。理想一串点,现实一条线。
我们把这个逻辑放到手机屏幕上。
手机屏幕上的最小显示单位就是像素了,一个 1920 * 1080 的屏幕指的就是各方向上像素点的数量。
假如绘制一条和屏幕一样宽的线段,一个点最小就算一个像素,最多也就 1080 个点了。
点占的像素越多,那么实际绘制时需要的点的数量越少,这也算是潜在的优化项了。
说完直线,再回到贝塞尔曲线上。
曲线和直线都有一个共同点,它们都有各自特定的方程,只不过我们用的直线例子比较简单,既 y = x ,一眼看出计算结果。
直线方程 y = x,在数学上可以这么描述:y 是关于 x 的函数,既 y = F(x) ,其中 x 的取值决定了该直线的长度。
根据上面的理解,这个长度的直线实际又是由在 x 的取值范围内对应的无数个点组成的。
反观贝塞尔曲线方程以及对应的图形如下:
- 二阶贝塞尔曲线:其中,P0 和 P2 是起始点,P1 是控制点。


- 三阶贝塞尔曲线其中,P0 和 P3 是起始点,P1 和 P2 是控制点。


不难理解,假设我们要绘制一条曲线,肯定要有起始和结束点来指定曲线的范围曲线。
而控制点就是指定该曲线的弧度,或者说指定该曲线的弯曲走向,不同的控制点得出的曲线绘制结果是不一样的。
另外,可以观察到,无论是几阶贝塞尔曲线,都会有参数 t 以及 t 的取值范围限定。
t 在 0~1 范围的闭区间内,那么 t 的取值个数实际上就有无数个了,这时的 t 就可以理解成上面介绍直线中讲到的 x 。
这样一来,就可以把起始点、控制点当初固定参数,那么贝塞尔曲线计算公式就成了 B = F(t) ,B 是关于 t 的函数,而 t 的取值范围为 0~1 的闭区间。
也就是说贝塞尔曲线,选定了起始点和控制点,照样可以看成是 t 在 0~1 闭区间内对应的无数个点所组成的。
有了上面的阐述,在工(ban)程(zhuan)的角度上,就不难理解贝塞尔曲线到底怎么使用了。
Android 绘制贝塞尔曲线
Android 自带贝塞尔曲线绘制 API ,通过 Path 类的 quadTo 和 cubicTo 方法就可以完成绘制。
1 // 构建 path 路径,也就是选取
2 path.reset();
3 path.moveto(p0x, p0y);
4 // 绘制二阶贝塞尔曲线
5 path.quadTo(p1x, p1y, p2x, p2y);
6 path.moveto(p0x, p0y);
7 path.close();
8
9 // 最后的绘制操作
10 canvas.drawPath(path, paint);
这里的绘制实际上就是把贝塞尔曲线计算的方程式交给了 Android 系统内部去完成了,参数传递上只传递了起始点和控制点。
我们可以通过自己的代码来计算这个方程式从而对逻辑上获得更多控制权,也就是把曲线拆分成许多个点组成,如果点的尺寸比较大,甚至可以减少点的个数实现同样的效果,达到绘制优化的目的。
OpenGL 绘制
通过 OpenGL 可以实现我们上述的方案,把曲线拆分成多个点组成。这种方案要求我们在 cpu 上去计算贝塞尔曲线方程,根据 t 的每一个取值,计算出一个贝塞尔点,用 OpenGL 去绘制上这个点。
这个点的绘制可以采用 OpenGL 中画三角形 GL_TRIANGLES 的形式去绘制,这样就可以给点带上纹理效果,不过这里面的坑略多,起始点和控制点都是运行时动态可变的实现难度会大于固定不变的。
这里先介绍另一种方案,这种方案实现比较简单也能达到优化效果,我们可以把贝塞尔曲线的计算方程式交给 GPU, 在 OpenGL Shader 中去完成。
这样一来,我们只要给定起始点和控制点,中间计算贝塞尔曲线去填补点的过程就交给 Shader 去完成了。
另外,通过控制 t 的数量,我们可以控制贝塞尔点填补的疏密。
t 越大,填补的点越多,超过一定阈值后,不会对绘制效果有提升,反而影响性能。
t 越小,那么贝塞尔曲线就退化成一串点组成了。所以说 t 的取值范围也能对绘制起到优化作用。
绘制效果如下图所示:

以下就是实际的代码部分了,关于 OpenGL 的基础理论部分可以参考之前写过的文章和公众号,就不再阐述了。
在 Shader 中定义一个函数,实现贝塞尔方程:
1vec2 fun(in vec2 p0, in vec2 p1, in vec2 p2, in vec2 p3, in float t){
2 float tt = (1.0 - t) * (1.0 -t);
3 return tt * (1.0 -t) *p0
4 + 3.0 * t * tt * p1
5 + 3.0 * t *t *(1.0 -t) *p2
6 + t *t *t *p3;
7}
该方程可以利用 Shader 中自带的函数优化一波:
1vec2 fun2(in vec2 p0, in vec2 p1, in vec2 p2, in vec2 p3, in float t)
2{
3 vec2 q0 = mix(p0, p1, t);
4 vec2 q1 = mix(p1, p2, t);
5 vec2 q2 = mix(p2, p3, t);
6 vec2 r0 = mix(q0, q1, t);
7 vec2 r1 = mix(q1, q2, t);
8 return mix(r0, r1, t);
9}
接下来就是具体的顶点着色器 shader :
1// 对应 t 数据的传递
2attribute float aData;
3// 对应起始点和结束点
4uniform vec4 uStartEndData;
5// 对应控制点
6uniform vec4 uControlData;
7// mvp 矩阵
8uniform mat4 u_MVPMatrix;
9
10void main() {
11 vec4 pos;
12 pos.w = 1.0;
13 // 取出起始点、结束点、控制点
14 vec2 p0 = uStartEndData.xy;
15 vec2 p3 = uStartEndData.zw;
16 vec2 p1 = uControlData.xy;
17 vec2 p2 = uControlData.zw;
18 // 取出 t 的值
19 float t = aData;
20 // 计算贝塞尔点的函数调用
21 vec2 point = fun2(p0, p1, p2, p3, t);
22 // 定义点的 x,y 坐标
23 pos.xy = point;
24 // 要绘制的位置
25 gl_Position = u_MVPMatrix * pos;
26 // 定义点的尺寸大小
27 gl_PointSize = 20.0;
28}
代码中的 uStartEndData 对应起始点和结束点,uControlData 对应两个控制点。
这两个变量的数据传递通过 gluniform4f 方法就好了:
1 mStartEndHandle = glGetUniformlocation(mProgram, "uStartEndData");
2 mControlHandle = glGetUniformlocation(mProgram, "uControlData");
3 // 传递数据,作为固定值
4 gluniform4f(mStartEndHandle,
5 mStartEndPoints[0],
6 mStartEndPoints[1],
7 mStartEndPoints[2],
8 mStartEndPoints[3]);
9 gluniform4f(mControlHandle,
10 mControlPoints[0],
11 mControlPoints[1],
12 mControlPoints[2],
13 mControlPoints[3]);
另外重要的变量就是 aData 了,它对应的就是 t 在 0~1 闭区间的划分的数量。
1 private float[] genTData() {
2 float[] tData = new float[Const.NUM_POINTS];
3 for (int i = 0; i < tData.length; i ++) {
4 float t = (float) i / (float) tData.length;
5 tData[i] = t;
6 }
7 return tData;
8 }
以上函数就是把 t 在 0~1 闭区间分成 Const.NUM_POINTS 份,每一份的值都存在 tData 数组中,最后通过 glVertexAttribPointer 函数传递给 Shader 。
最后实际绘制时,我们采用 GL_POINTS 的形式绘制就好了。
1 GLES20.glDrawArrays(GLES20.GL_POINTS, 0, Const.NUM_POINTS );
以上就是 OpenGL 绘制贝塞尔曲线的小实践。

Android Flutter利用贝塞尔曲线画一个小海豚
前言
贝塞尔曲线的应用填补了计算机绘制与手绘之前的差距,更能表达人想画出的曲线,为了更好的理解万能的贝塞尔曲线,而海豚是我认为在海洋生物中身体曲线最完美的海洋生物,在海洋中游泳速度最高可达80km/h;比驱逐舰速度还快,学习绘制正好学到了贝塞尔曲线,那么我们今天就用贝塞尔曲线画看看能不能画一只可爱的小海豚呢。
效果图
先上效果图:

实现步骤
path路径绘制贝塞尔曲线的方法非常简单,只需要传入控制点即可,二阶就传1个控制点1个终点,三阶就传2个控制点和1个终点,但是要找到合适控制的点就没那么容易了,这时候我们如果可以用手指在屏幕上不断调试寻找合适的点岂不是非常方便,接下来我们就先实现下面的功能,通过手指不断调试控制点位并将多个贝塞尔曲线进行连接。

可以看到一个三阶贝塞尔需要1个起点、2个控制点和1个终点组成,首先我们需要通过手势识别将这些控制点存储起来然后赋值给绘制组件进行更新就可以了,这里我们需要用到状态管理ChangeNotifier类,它继承Listenable,因为在绘制组件的构造方法里有一个参数repaint接受Listenable类型来控制是否重新绘制,数据变化就重新绘制。
const CustomPainter({ Listenable? repaint }) : _repaint = repaint;因为CustomPainter的构造方法里的repaint参数就是负责更新绘制的,所以我们先要定义一个类继承ChangeNotifier来存储这些数据。
代码:
class TouchController extends ChangeNotifier {
List<Offset> _points = []; //点集合
int _selectIndex = -1;// 选中的点 更新位置用
int get selectIndex => _selectIndex;
List<Offset> get points => _points;
// 选择某一个点 保存index
set selectIndex(int value) {
if (_selectIndex == value) return;
_selectIndex = value;
notifyListeners();// 通知刷新
}
// 选中的点标记
Offset? get selectPoint => _selectIndex == -1 ? null : _points[_selectIndex];
// 添加一个点
void addPoint(Offset point) {
points.add(point);
notifyListeners();
}
// 手指移动时更新当前点的位置
void updatePoint(int index, Offset point) {
points[index] = point;
notifyListeners();
}
// 删除最后一个点 相当于撤回上一步操作
void removeLast() {
points.removeLast();
notifyListeners();
}
}有了存储数据的空间之后,我们就需要通过手势去获取这些点,通过手势在画布上的操作获取当前的位置进行存储以及更新。
GestureDetector(
child: CustomPaint(
painter:
_DolphinPainter(widget.touchController, widget.image),
),
onPanDown: (d) {
// 按压
judgeZone(d.localPosition);
},
onPanUpdate: (d) {
// 移动
if (widget.touchController.selectIndex != -1) {
widget.touchController.updatePoint(
widget.touchController.selectIndex, d.localPosition);
}
},
)
///判断出是否在某点的半径为r圆范围内
bool judgeCircleArea(Offset src, Offset dst, double r) =>
(src - dst).distance <= r;
///手指按下触发
void judgeZone(Offset src) {
/// 循环所有的点
for (int i = 0; i < widget.touchController.points.length; i++) {
// 判断手指按的位置有没有按过的点
if (judgeCircleArea(src, widget.touchController.points[i], 20)) {
// 有点 不添加更新选中的点
widget.touchController.selectIndex = i;
return;
}
}
// 无点 添加新的点 并将选中的点清空
widget.touchController.addPoint(src);
widget.touchController.selectIndex = -1;
}到这里我们的手势按压和移动就会将数据存储到我们刚才定义的类中,接下来我们需要将这些数据赋予真正的绘制组件 CustomPainter。
class _DolphinPainter extends CustomPainter {
final TouchController touchController;// 存储数据类
// final ui.Image image;
_DolphinPainter(this.touchController, this.image)
// 这个地方传入需要更新的 Listenable
: super(repaint: touchController);
List<Offset>? pos; //存储手势按压的点
@override
void paint(Canvas canvas, Size size) {
// 画布原点平移到屏幕中央
canvas.translate(size.width / 2, size.height / 2);
// ,因为手势识别的原点是左上角,所以这里将存储的点相对的原点进行偏移到跟画布一致 负值向左上角偏移
pos = touchController.points
.map((e) => e.translate(-size.width / 2, -size.height / 2))
.toList();
// 定义画笔
var paint = Paint()
..strokeWidth = 2
..color = Colors.purple
..style = PaintingStyle.stroke
..isAntiAlias = true;
// canvas.drawImage(image, Offset(-image.width / 2, -image.height / 2), paint);
// 如果点小于4个 那么就只绘制点 如果>=4个点 那么就绘制贝塞尔曲线
if (pos != null && pos!.length >= 4) {
var path = Path();
// 设置起点 手指第一个按压的点
path.moveTo(pos![0].dx, (pos![0].dy));
// path添加第一个贝塞尔曲线
path.cubicTo(pos![1].dx,pos![1].dy, pos![2].dx, pos![2].dy, pos![3].dx,
pos![3].dy);
//绘制辅助线
_drawHelpLine(canvas, size, paint, 0);
// 绘制首个贝塞尔曲线
canvas.drawPath(path, paint..color = Colors.purple);
// for循环 绘制第2个以后的曲线 以上个终点为下一个的起点
for (int i = 1; i < (pos!.length - 1) ~/ 3; i++) {
//之后贝塞尔曲线的起点都是上一个贝塞尔曲线的终点
// 比如第一个曲线 1,2,3,4.第二个就是4,5,6,7...以此类推,这样我们才能把线连接起来绘制图案
// 这里把绘制之前的颜色覆盖
// canvas.drawPath(path, paint..color = Colors.white);
// 绘制辅助线
_drawHelpLine(canvas, size, paint, i);
//绘制贝塞尔曲线
path.cubicTo(
pos![i * 3 + 1].dx,
pos![i * 3 + 1].dy,
pos![i * 3 + 2].dx,
pos![i * 3 + 2].dy,
pos![i * 3 + 3].dx,
pos![i * 3 + 3].dy,
);
if (i == 8) {
path.close();
}
canvas.drawPath(path, paint..color = Colors.purple);
}
// 绘制辅助点
_drawHelpPoint(canvas, paint);
// 选中点
_drawHelpSelectPoint(canvas, size, paint);
} else {
// 绘制辅助点
_drawHelpPoint(canvas, paint);
}
// 画眼睛 眼睛位于起点的左侧,所以中心点向左偏移
canvas.drawCircle(
pos!.first.translate(-50, 5),
10,
paint
..color = Colors.black87
..style = PaintingStyle.stroke
..strokeWidth = 2);
canvas.drawCircle(
pos!.first.translate(-53, 5),
7,
paint
..color = Colors.black87
..style = PaintingStyle.fill);
}
@override
bool shouldRepaint(covariant CustomPainter oldDelegate) {
return false;
}
void _drawHelpPoint(Canvas canvas, Paint paint) {
canvas.drawPoints(
PointMode.points,
pos ?? [],
paint
..strokeWidth = 10
..strokeCap = StrokeCap.round
..color = Colors.redAccent);
}
void _drawHelpSelectPoint(Canvas canvas, Size size, Paint paint) {
Offset? selectPos = touchController.selectPoint;
selectPos = selectPos?.translate(-size.width / 2, -size.height / 2);
if (selectPos == null) return;
canvas.drawCircle(
selectPos,
10,
paint
..color = Colors.green
..strokeWidth = 2);
}
void _drawHelpLine(Canvas canvas, Size size, Paint paint, int i) {
canvas.drawLine(
Offset(pos![i * 3].dx, pos![i * 3].dy),
Offset(pos![i * 3 + 1].dx, pos![i * 3 + 1].dy),
paint
..color = Colors.redAccent
..strokeWidth = 2);
canvas.drawLine(
Offset(pos![i * 3 + 1].dx, pos![i * 3 + 1].dy),
Offset(pos![i * 3 + 2].dx, pos![i * 3 + 2].dy),
paint
..color = Colors.redAccent
..strokeWidth = 2);
canvas.drawLine(
Offset(pos![i * 3 + 2].dx, pos![i * 3 + 2].dy),
Offset(pos![i * 3 + 3].dx, pos![i * 3 + 3].dy),
paint
..color = Colors.redAccent
..strokeWidth = 2);
}最终在我们的手指的控制以及辅助线的帮助下,图案就慢慢的绘制出来了。

去掉辅助线和点

然后将画笔改为填充,那么就得到我们一开始那副可爱的小海豚了。
总结
通过这个小海豚图案我们可以更加的理解贝塞尔曲线的绘制机制,通过你的手势控制,你也可以画出任何曲线和任何图案,可以说贝塞尔曲线就是绘制中的灵魂,掌握了贝塞尔曲线就相当于掌握了所有绘制组件,因为理论上来说,所有的二维图形都可以被贝塞尔曲线画出来,只要我们能准确的找到控制的点,就可以绘制无限可能的图案。
以上就是Android Flutter利用贝塞尔曲线画一个小海豚的详细内容,更多关于Android Flutter海豚的资料请关注其它相关文章!
- android贝塞尔曲线实现波浪效果
- Android贝塞尔曲线实现手指轨迹
- Android贝塞尔曲线实现直播点赞效果
- Android Path绘制贝塞尔曲线实现QQ拖拽泡泡
- Android中贝塞尔曲线的绘制方法示例代码

Android Path绘制贝塞尔曲线实现QQ拖拽泡泡
这两天学习了使用Path绘制贝塞尔曲线相关,然后自己动手做了一个类似QQ未读消息可拖拽的小气泡,效果图如下:

最终效果图
接下来一步一步的实现整个过程。
基本原理
其实就是使用Path绘制三点的二次方贝塞尔曲线来完成那个妖娆的曲线的。然后根据触摸点不断绘制对应的圆形,根据距离的改变改变原始固定圆形的半径大小。最后就是松手后返回或者爆裂的实现。
Path介绍:
顾名思义,就是一个路径的意思,Path里面有很多的方法,本次设计主要用到的相关方法有
- moveto() 移动Path到一个指定的点
- quadTo() 绘制二次贝塞尔曲线,接收两个点,第一个是控制弧度的点,第二个是终点。
- lineto() 就是连线
- close() 闭合Path路径,
- reset() 重置Path的相关设置
Path入门热身:
path.reset(); path.moveto(200,200); //第一个坐标是对应的控制的坐标,第二个坐标是终点坐标 path.quadTo(400,250,600,200); canvas.drawPath(path,paint); canvas.translate(0,200); //调用close,就会首尾闭合连接 path.close(); canvas.drawPath(path,paint);
记得不要在onDraw方法中new Path或者 Paint哟!

Path
具体实现拆分:
其实整个过程就是绘制了两个贝塞尔二次曲线的的闭合Path路径,然后在上面添加两个圆形。


闭合的Path 路径实现从左上点画二次贝塞尔曲线到左下点,左下点连线到右下点,右下点二次贝塞尔曲线到右上点,最后闭合一下!!
相关坐标的确定
这是这次里面的难点之一,因为涉及到了数学里面的一个sin,cos,tan等等,我其实也忘完了,然后又脑补了一下,废话不多说,

为什么自己要亲自去画一下呢,因为画了你才知道,在360旋转的过程中,角标体系是有两套的,如果就使用一套来画的话,就画出现在旋转的过程中曲线重叠在一起的情况!
问题已经抛出来了,接下来直接看看代码实现!
角度确定
根据贴出来的原理图可以知道,我们可以使用起始圆心坐标和拖拽的圆心坐标,根据反正切函数来得到具体的弧度。
int dy = Math.abs(CIRCLEY - startY); int dx = Math.abs(CIRCLEX - startX); angle = Math.atan(dy * 1.0 / dx);
ok,这里的startX,Y就是移动过程中的坐标。angle就是得到的对应的弧度(角度)。
相关Path绘制
前面已经提到在旋转的过程中有两套坐标体系,一开始我也很纠结这个坐标体系要怎么确定,后面又恍然大悟,其实相当于就是一三象限正比例增长,二四象限,反比例增长。
flag = (startY - CIRCLEY ) * (startX- CIRCLEX ) <= 0;
//增加一个flag,用于判断使用哪种坐标体系。
最最重要的来了,绘制相关的Path路径!
path.reset();
if (flag) {
//第一个点
path.moveto((float) (CIRCLEX - Math.sin(angle) * ORIGIN_RAdio),(float) (CIRCLEY - Math.cos(angle) * ORIGIN_RAdio));
path.quadTo((float) ((startX + CIRCLEX) * 0.5),(float) ((startY + CIRCLEY) * 0.5),(float) (startX - Math.sin(angle) * DRAG_RAdio),(float) (startY - Math.cos(angle) * DRAG_RAdio));
path.lineto((float) (startX + Math.sin(angle) * DRAG_RAdio),(float) (startY + Math.cos(angle) * DRAG_RAdio));
path.quadTo((float) ((startX + CIRCLEX) * 0.5),(float) (CIRCLEX + Math.sin(angle) * ORIGIN_RAdio),(float) (CIRCLEY + Math.cos(angle) * ORIGIN_RAdio));
path.close();
canvas.drawPath(path,paint);
} else {
//第一个点
path.moveto((float) (CIRCLEX - Math.sin(angle) * ORIGIN_RAdio),(float) (CIRCLEY + Math.cos(angle) * ORIGIN_RAdio));
path.quadTo((float) ((startX + CIRCLEX) * 0.5),(float) (startY + Math.cos(angle) * DRAG_RAdio));
path.lineto((float) (startX + Math.sin(angle) * DRAG_RAdio),(float) (startY - Math.cos(angle) * DRAG_RAdio));
path.quadTo((float) ((startX + CIRCLEX) * 0.5),(float) (CIRCLEY - Math.cos(angle) * ORIGIN_RAdio));
path.close();
canvas.drawPath(path,paint);
}
这里的代码就是把图片上相关的数学公式Java化而已!
到这里,其实主要的工作就完成的差不多了!
接下来,设置paint 为填充的效果,最后再画两个圆
paint.setStyle(Paint.Style.FILL) canvas.drawCircle(CIRCLEX,CIRCLEY,ORIGIN_RAdio,paint);//默认的 canvas.drawCircle(startX == 0 ? CIRCLEX : startX,startY == 0 ? CIRCLEY : startY,DRAG_RAdio,paint);//拖拽的
就可以绘制出想要的效果了!
这里不得不再说说onTouch的处理!
case MotionEvent.ACTION_DOWN://有事件先拦截再说!! getParent().requestdisallowInterceptTouchEvent(true); CurrentState = STATE_IDLE; animsetXY.cancel(); startX = (int) ev.getX(); startY = (int) ev.getRawY(); break;
处理一下事件分发的坑!
测量和布局
这样基本过得去了,但是我们的布局什么的还没有处理,math_parent是万万没法使用到具体项目当中去的!
测量的时候,如果发现不是精准模式,那么都手动去计算出需要的宽度和高度。
@Override
protected void onMeasure(int widthMeasureSpec,int heightMeasureSpec) {
int modeWidth = MeasureSpec.getMode(widthMeasureSpec);
int modeHeight = MeasureSpec.getMode(heightMeasureSpec);
if (modeWidth == MeasureSpec.UNSPECIFIED || modeWidth == MeasureSpec.AT_MOST) {
widthMeasureSpec = MeasureSpec.makeMeasureSpec(DEFAULT_RAdio * 2,MeasureSpec.EXACTLY);
}
if (modeHeight == MeasureSpec.UNSPECIFIED || modeHeight == MeasureSpec.AT_MOST) {
heightMeasureSpec = MeasureSpec.makeMeasureSpec(DEFAULT_RAdio * 2,MeasureSpec.EXACTLY);
}
super.onMeasure(widthMeasureSpec,heightMeasureSpec);
}
然后在布局变化时,获取相关坐标,确定初始圆心坐标:
@Override
protected void onSizeChanged(int w,int h,int oldw,int oldh) {
super.onSizeChanged(w,h,oldw,oldh);
CIRCLEX = (int) ((w) * 0.5 + 0.5);
CIRCLEY = (int) ((h) * 0.5 + 0.5);
}
然后清单文件里面就可以这样配置了:
<com.lovejjfg.circle.DragBubbleView android:id="@+id/dbv" android:layout_width="wrap_content" android:layout_height="wrap_content" android:layout_gravity="center"/>
这样之后,又会出现一个问题,那就是wrap_content 之后,这个View能绘制的区域只有自身那么大了,拖拽了都看不见了!这个坑怎么办呢,其实很简单,父布局加上android:clipChildren="false" 的属性!
这个坑也算是解决了!!
相关状态的确定
我们是不希望它可以无限的拖拽的,就是有一个拖拽的最远距离,还有就是放手后的返回,爆裂。那么对应的,这里需要确定几种状态:
private final static int STATE_IDLE = 1;//静止的状态 private final static int STATE_DRAG_norMAL = 2;//正在拖拽的状态 private final static int STATE_DRAG_BREAK = 3;//断裂后的拖拽状态 private final static int STATE_UP_BREAK = 4;//放手后的爆裂的状态 private final static int STATE_UP_BACK = 5;//放手后的没有断裂的返回的状态 private final static int STATE_UP_DRAG_BREAK_BACK = 6;//拖拽断裂又返回的状态 private int CurrentState = STATE_IDLE; private int MIN_RAdio = (int) (ORIGIN_RAdio * 0.4);//最小半径 private int MAXdisTANCE = (int) (MIN_RAdio * 13);//最远的拖拽距离
确定好这些之后,在move的时候,就要去做相关判断了:
case MotionEvent.ACTION_MOVE://移动的时候
startX = (int) ev.getX();
startY = (int) ev.getY();
updatePath();
invalidate();
break;
private void updatePath() {
int dy = Math.abs(CIRCLEY - startY);
int dx = Math.abs(CIRCLEX - startX);
double dis = Math.sqrt(dy * dy + dx * dx);
if (dis <= MAXdisTANCE) {//增加的情况,原始半径减小
if (CurrentState == STATE_DRAG_BREAK || CurrentState == STATE_UP_DRAG_BREAK_BACK) {
CurrentState = STATE_UP_DRAG_BREAK_BACK;
} else {
CurrentState = STATE_DRAG_norMAL;
}
ORIGIN_RAdio = (int) (DEFAULT_RAdio - (dis / MAXdisTANCE) * (DEFAULT_RAdio - MIN_RAdio));
Log.e(TAG,"distance: " + (int) ((1 - dis / MAXdisTANCE) * MIN_RAdio));
Log.i(TAG,"distance: " + ORIGIN_RAdio);
} else {
CurrentState = STATE_DRAG_BREAK;
}
// distance = dis;
flag = (startY - CIRCLEY) * (startX - CIRCLEX) <= 0;
Log.i("TAG","updatePath: " + flag);
angle = Math.atan(dy * 1.0 / dx);
}
updatePath() 的方法之前已经看过部分了,这次的就是完整的。
这里做的事就是根据拖拽的距离更改相关的状态,并根据百分比来修改原始圆形的半径大小。还有就是之前介绍的确定相关的弧度!
最后放手的时候:
case MotionEvent.ACTION_UP:
if (CurrentState == STATE_DRAG_norMAL) {
CurrentState = STATE_UP_BACK;
valueX.setIntValues(startX,CIRCLEX);
valueY.setIntValues(startY,CIRCLEY);
animsetXY.start();
} else if (CurrentState == STATE_DRAG_BREAK) {
CurrentState = STATE_UP_BREAK;
invalidate();
} else {
CurrentState = STATE_UP_DRAG_BREAK_BACK;
valueX.setIntValues(startX,CIRCLEY);
animsetXY.start();
}
break;
自动返回这里使用到的 ValueAnimator,
animsetXY = new AnimatorSet();
valueX = ValueAnimator.ofInt(startX,CIRCLEX);
valueY = ValueAnimator.ofInt(startY,CIRCLEY);
animsetXY.playTogether(valueX,valueY);
valueX.setDuration(500);
valueY.setDuration(500);
valueX.setInterpolator(new OvershootInterpolator());
valueY.setInterpolator(new OvershootInterpolator());
valueX.addUpdateListener(new ValueAnimator.AnimatorUpdateListener() {
@Override
public void onAnimationUpdate(ValueAnimator animation) {
startX = (int) animation.getAnimatedValue();
Log.e(TAG,"onAnimationUpdate-startX: " + startX);
invalidate();
}
});
valueY.addUpdateListener(new ValueAnimator.AnimatorUpdateListener() {
@Override
public void onAnimationUpdate(ValueAnimator animation) {
startY = (int) animation.getAnimatedValue();
Log.e(TAG,"onAnimationUpdate-startY: " + startY);
invalidate();
}
});
最后在看看完整的onDraw方法吧!
@Override
protected void onDraw(Canvas canvas) {
switch (CurrentState) {
case STATE_IDLE://空闲状态,就画默认的圆
if (showCircle) {
canvas.drawCircle(CIRCLEX,paint);//默认的
}
break;
case STATE_UP_BACK://执行返回的动画
case STATE_DRAG_norMAL://拖拽状态 画贝塞尔曲线和两个圆
path.reset();
if (flag) {
//第一个点
path.moveto((float) (CIRCLEX - Math.sin(angle) * ORIGIN_RAdio),(float) (CIRCLEY - Math.cos(angle) * ORIGIN_RAdio));
path.quadTo((float) ((startX + CIRCLEX) * 0.5),(float) (startY - Math.cos(angle) * DRAG_RAdio));
path.lineto((float) (startX + Math.sin(angle) * DRAG_RAdio),(float) (startY + Math.cos(angle) * DRAG_RAdio));
path.quadTo((float) ((startX + CIRCLEX) * 0.5),(float) (CIRCLEY + Math.cos(angle) * ORIGIN_RAdio));
path.close();
canvas.drawPath(path,paint);
} else {
//第一个点
path.moveto((float) (CIRCLEX - Math.sin(angle) * ORIGIN_RAdio),(float) (CIRCLEY + Math.cos(angle) * ORIGIN_RAdio));
path.quadTo((float) ((startX + CIRCLEX) * 0.5),(float) (startY + Math.cos(angle) * DRAG_RAdio));
path.lineto((float) (startX + Math.sin(angle) * DRAG_RAdio),(float) (startY - Math.cos(angle) * DRAG_RAdio));
path.quadTo((float) ((startX + CIRCLEX) * 0.5),(float) (CIRCLEY - Math.cos(angle) * ORIGIN_RAdio));
path.close();
canvas.drawPath(path,paint);
}
if (showCircle) {
canvas.drawCircle(CIRCLEX,paint);//默认的
canvas.drawCircle(startX == 0 ? CIRCLEX : startX,paint);//拖拽的
}
break;
case STATE_DRAG_BREAK://拖拽到了上限,画拖拽的圆:
case STATE_UP_DRAG_BREAK_BACK:
if (showCircle) {
canvas.drawCircle(startX == 0 ? CIRCLEX : startX,paint);//拖拽的
}
break;
case STATE_UP_BREAK://画出爆裂的效果
canvas.drawCircle(startX - 25,startY - 25,10,circlePaint);
canvas.drawCircle(startX + 25,startY + 25,circlePaint);
canvas.drawCircle(startX,startY,18,circlePaint);
canvas.drawCircle(startX - 25,circlePaint);
break;
}
}
到这里,成品就出来了!!
总结:
1、确定默认圆形的坐标;
2、根据move的情况,实时获取最新的坐标,根据移动的距离(确定出角度),更新相关的状态,画出相关的Path路径。超出上限,不再画Path路径。
3、松手时,根据相关的状态,要么带Path路径执行动画返回,要么不带Path路径直接返回,要么直接爆裂!
以上就是用Android Path 绘制贝塞尔曲线的示例,后续继续补充相关文章,谢谢大家对本站的支持!

Android 之二阶贝塞尔曲线的波浪头像 (三阶的爱心飞出)
1、写这个 demo 主要是因为一个同事给我看了一个 ios 的效果,因为感觉好玩所以我就写了 android 样式的,具体的效果就如下图展示(图是 ios 的 gif 不过效果是一样的),有需要的朋友在下面会给出下载地址
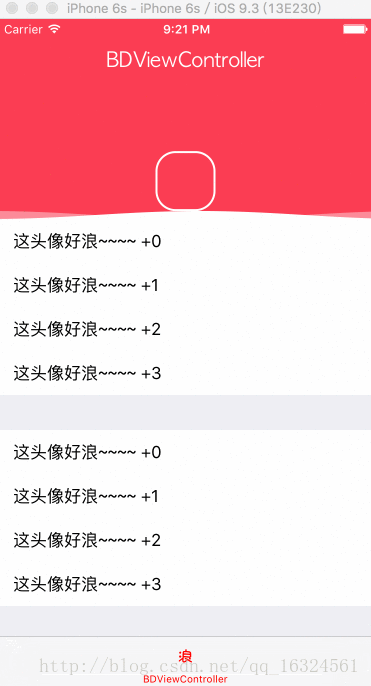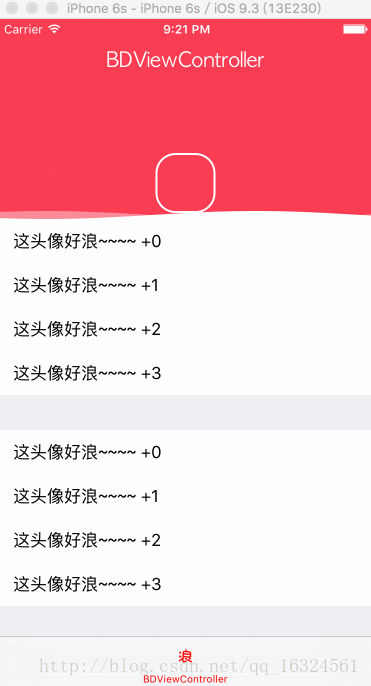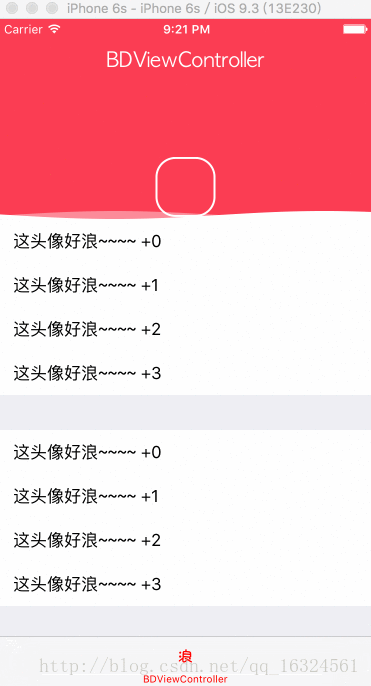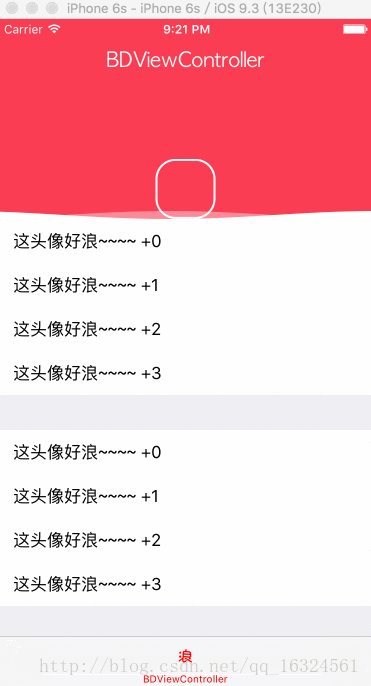
首先分析一下我的做法,我是将波浪的部分和头像分开考虑,根据波浪的移动高度将头像画出

一、定义属性
其实我在做的时候我是直接开始画,画完了才去优化自定义属性,然而现在这些过程已经不重要了,我就先介绍下定义的属性分别都是什么含义。
<mmf.com.bubblingdemo.CorrugateView
android:id="@+id/cv_waves"
android:layout_width="match_parent"
android:layout_marginTop="100dp"
app:imgSize="50dp"
app:waveHeight="20dp"
app:rollTime="20"
app:rollDistance="5"
android:layout_height="70dp" />app:imgSize=”50dp” 定义的是头像的大小
app:waveHeight=”20dp” 波浪的高度
app:rollTime=”20” 移动一次的时间
app:rollDistance=”5” 移动一次的距离,像素
二、开始画 CorrugateView 这个控件
(1)获取所有属性的值和初始化所需要的画笔
public void init(Context context, AttributeSet attrs) {
TypedArray attr = context.getTheme().obtainStyledAttributes(attrs, R.styleable.CorrugateView, 0, 0);
try {
imgSize = (int) attr.getDimension(R.styleable.CorrugateView_imgSize, getResources().getDimensionPixelSize(
R.dimen.top_distance));
waveHeight = (int) attr.getDimension(R.styleable.CorrugateView_waveHeight, getResources().getDimensionPixelSize(
R.dimen.top_distance_20));
rollTime = attr.getInteger(R.styleable.CorrugateView_rollTime, 30);
rollDistance = attr.getInteger(R.styleable.CorrugateView_rollDistance, 5);
} finally {
attr.recycle();
}
length = rollDistance;
//保存上面一条曲线的数组
mPointsList = new ArrayList<Point>();
//保存下面一条曲线的数组
mPointsListBottom = new ArrayList<Point>();
//画上面曲线的画笔和线
mWavePath = new Path();
mPaint = new Paint();
mPaint.setAntiAlias(true);
mPaint.setStyle(Paint.Style.FILL);
mPaint.setColor(getResources().getColor(R.color.white));
//画下面曲线的画笔和线
mWavePathBottom = new Path();
mPaintBottom = new Paint();
mPaintBottom.setAntiAlias(true);
mPaintBottom.setStyle(Paint.Style.FILL);
mPaintBottom.setColor(getResources().getColor(R.color.top_withe));
}(2)获取控件的宽高和初始化要画的波浪的每个点
@Override
protected void onMeasure(int widthMeasureSpec, int heightMeasureSpec) {
super.onMeasure(widthMeasureSpec, heightMeasureSpec);
mWidth = getMeasuredWidth();
//控件高度=图片的高度加上波浪的高度
mHeight = waveHeight + imgSize;
//初始化每个点
initPoint();
invalidate();
//开启一个计时器
if (timer == null)
start();
}initPoint (); 这个方法就是画二阶贝塞尔曲线的每个点,具体看代码,因为有点长就不贴进来了
start ();开启一个计时器,主要作用是在一定时间按一定的距离将曲线向右移动
(3)画曲线
@Override
protected void onDraw(Canvas canvas) {
//画两条曲线
mWavePath.reset();
mWavePathBottom.reset();
mWavePathBottom.moveTo(mPointsListBottom.get(0).x, mPointsListBottom.get(0).y);
mWavePathBottom.quadTo(mPointsListBottom.get(1).x, mPointsListBottom.get(1).y, mPointsListBottom.get(2).x, mPointsListBottom.get(2).y);
mWavePathBottom.quadTo(mPointsListBottom.get(3).x, mPointsListBottom.get(3).y, mPointsListBottom.get(4).x, mPointsListBottom.get(4).y);
mWavePathBottom.quadTo(mPointsListBottom.get(5).x, mPointsListBottom.get(5).y, mPointsListBottom.get(6).x, mPointsListBottom.get(6).y);
mWavePathBottom.quadTo(mPointsListBottom.get(7).x, mPointsListBottom.get(7).y, mPointsListBottom.get(8).x, mPointsListBottom.get(8).y);
mWavePathBottom.quadTo(mPointsListBottom.get(9).x, mPointsListBottom.get(9).y, mPointsListBottom.get(10).x, mPointsListBottom.get(10).y);
mWavePathBottom.lineTo(mPointsListBottom.get(10).x, mHeight);
mWavePathBottom.lineTo(mPointsListBottom.get(0).x, mHeight);
mWavePathBottom.lineTo(mPointsListBottom.get(0).x, mPointsListBottom.get(0).y);
mWavePathBottom.close();
canvas.drawPath(mWavePathBottom, mPaintBottom);
mWavePath.moveTo(mPointsList.get(0).x, mPointsList.get(0).y);
mWavePath.quadTo(mPointsList.get(1).x, mPointsList.get(1).y, mPointsList.get(2).x, mPointsList.get(2).y);
mWavePath.quadTo(mPointsList.get(3).x, mPointsList.get(3).y, mPointsList.get(4).x, mPointsList.get(4).y);
mWavePath.quadTo(mPointsList.get(5).x, mPointsList.get(5).y, mPointsList.get(6).x, mPointsList.get(6).y);
mWavePath.quadTo(mPointsList.get(7).x, mPointsList.get(7).y, mPointsList.get(8).x, mPointsList.get(8).y);
mWavePath.lineTo(mPointsList.get(8).x, mHeight);
mWavePath.lineTo(mPointsList.get(0).x, mHeight);
mWavePath.lineTo(mPointsList.get(0).x, mPointsList.get(0).y);
mWavePath.close();
canvas.drawPath(mWavePath, mPaint);
//画头像
Bitmap bitmap = BitmapFactory.decodeResource(this.getContext()
.getResources(), R.mipmap.icon_2017);
drawImage(canvas, bitmap, (mWidth - imgSize) / 2, (int) getHeigthIcon() - imgSize,
imgSize, imgSize, 0, 0, mPaint);
//当移动的长度大于等于屏幕宽度重置点的坐标
if (allLength >= mWidth) {
resetPoints();
allLength = 0;
}
}getHeigthIcon() 这个方法比较重要,控制着头像的上下移动,主要运用贝塞尔曲线的二阶公式计算头像的高度,下图所示
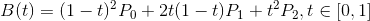
/** * 获取头像中心的x对应的曲线的y值 * @return */
private float getHeigthIcon() {
//移动的比率
float t = (float) allHeight * 2 / mWidth;
float y;
//ismHeight为true表示向下移动 false表示向上移动
if (ismHeight) {
//二价的贝塞尔曲线公式计算下面的曲线的根据t变化的高度
y = mPointsList.get(2).y * (1 - t) * (1 - t)
+ 2 * mPointsList.get(3).y * t * (1 - t)
+ mPointsList.get(4).y * t * t;
} else {
//二价的贝塞尔曲线公式计算上面的曲线的根据t变化的高度
y = mPointsList.get(0).y * (1 - t) * (1 - t)
+ 2 * mPointsList.get(1).y * t * (1 - t)
+ mPointsList.get(2).y * t * t;
}
return y;
}drawImage(Canvas canvas, Bitmap blt, int x, int y, int w,int h, int bx, int by, Paint paint) 画图片的方法,具体看代码,至此一个波浪的头像就算完成啦!感兴趣的下 demo 去看啦!
哦!差点忘了还有一个三阶的爱心,demo 的 LoveLayout.java 这个文件哟!感兴趣的自己去看哟!
效果效果图,我又忘了!如下所示,里面使用了透明度的渐变,所以越高就越透明了,每个爱心的路径都是一条随机的三阶贝塞尔曲线,demo 中只要点界面就会抛出一个爱心,自己去欣赏吧!

demo 下载地址:https://github.com/972242736/BubblingDemo.git

Android 贝塞尔曲线 折线图
1、贝塞尔曲线:http://baike.baidu.com/view/60154.htm,在这里理解什么是贝塞尔曲线
2、直接上图:

3、100多行代码就可以画出贝塞尔曲线,直接上代码
package com.example.bezier;
import java.util.ArrayList;
import java.util.List;
import android.app.Activity;
import android.content.Context;
import android.graphics.Canvas;
import android.graphics.Color;
import android.graphics.Paint;
import android.graphics.PathMeasure;
import android.graphics.Paint.Style;
import android.graphics.Path;
import android.os.Bundle;
import android.view.View;
import android.view.Window;
import android.view.WindowManager;
public class MainActivity extends Activity {
@Override
public void onCreate(Bundle savedInstanceState) {
super.onCreate(savedInstanceState);
requestwindowFeature(Window.FEATURE_NO_TITLE);
getwindow().setFlags(WindowManager.LayoutParams.FLAG_FULLSCREEN,WindowManager.LayoutParams.FLAG_FULLSCREEN);
setContentView(new BezierView(this));
}
}
class BezierView extends View {
/**
*
* @author liqiongwei
* @param context
*
*/
public BezierView(Context context) {
super(context);
}
protected void onDraw(Canvas canvas) {
List<Float> points = new ArrayList<Float>();
Paint paint = new Paint();
// 添加第一个点(118.0,294.0),points.add((float) 118.0);// X轴
points.add((float) 294.0);// Y轴
// 添加第二个点
points.add((float) 206.0);
points.add((float) 294.0);
// 添加第三个点
points.add((float) 294.0);
points.add((float) 118.0);
// 添加第四个点
points.add((float) 382.0);
points.add((float) 206.0);
points.add((float) 470.0);
points.add((float) 118.0);
// 通过画折线和贝塞尔曲线可以知道,点得位置是不一样的。
// 画折线
for (int i = 0; i < points.size() - 2; i = i + 2) {
canvas.drawLine(points.get(i),points.get(i + 1),points.get(i + 2),points.get(i + 3),paint);
canvas.drawCircle(points.get(i),3,paint);
}
canvas.drawCircle(points.get(points.size() - 2),points.get(points.size() - 1),paint);
// 贝塞尔曲线
paint.setColor(Color.BLUE);
Path p = new Path();
Point p1 = new Point();
Point p2 = new Point();
Point p3 = new Point();
float xp = points.get(0);
float yp = points.get(1);
// 设置第一个点开始
p.moveto(xp,yp);
int length = points.size();
// 设置第一个控制点33%的距离
float mFirstMultiplier = 0.3f;
// 设置第二个控制点为66%的距离
float mSecondMultiplier = 1 - mFirstMultiplier;
for (int b = 0; b < length; b += 2) {
int nextIndex = b + 2 < length ? b + 2 : b;
int nextNextIndex = b + 4 < length ? b + 4 : nextIndex;
// 设置第一个控制点
calc(points,p1,b,nextIndex,mSecondMultiplier);
// 设置第二个控制点
p2.setX(points.get(nextIndex));
p2.setY(points.get(nextIndex + 1));
// 设置第二个控制点
calc(points,p3,nextNextIndex,mFirstMultiplier);
// 最后一个点就是赛贝尔曲线上的点
p.cubicTo(p1.getX(),p1.getY(),p2.getX(),p2.getY(),p3.getX(),p3.getY());
// 画点
}
PathMeasure mPathMeasure;
mPathMeasure = new PathMeasure(p,false);
// 设置为线
paint.setStyle(Style.stroke);
reSetPointWithPath(mPathMeasure,points);
for (int k = 0; k < points.size()-1; k +=2) {
canvas.drawCircle(points.get(k),points.get(k+1),5,paint);
}
canvas.drawPath(p,paint);
invalidate();
}
/**
* 计算控制点
* @param points
* @param result
* @param index1
* @param index2
* @param multiplier
*/
private void calc(List<Float> points,Point result,int index1,int index2,final float multiplier) {
float p1x = points.get(index1);
float p1y = points.get(index1 + 1);
float p2x = points.get(index2);
float p2y = points.get(index2 + 1);
float diffX = p2x - p1x;
float diffY = p2y - p1y;
result.setX(p1x + (diffX * multiplier));
result.setY(p1y + (diffY * multiplier));
}
/**
* 重新设置点的位置,为曲线上的位置
* @param mPathMeasure
* @param pointsList
*/
public void reSetPointWithPath(PathMeasure mPathMeasure,List<Float> pointsList){
int length = (int) mPathMeasure.getLength();
int pointsLength = pointsList.size();
float[] coords = new float[2];
for (int b = 0; b < length; b++) {
mPathMeasure.getPosTan(b,coords,null);
double prevDiff = Double.MAX_VALUE;
boolean ok = true;
for (int j = 0; j < pointsLength && ok; j += 2) {
double diff = Math.abs(pointsList.get(j) - coords[0]);
if (diff < 1) {
pointsList.set(j + 1,coords[1]);
prevDiff = diff;
}
ok = prevDiff > diff;
}
}
}
}
4、定义点的类
package com.example.bezier;
import java.io.Serializable;
/**
* 点的类,来源于Achartengine
*/
public final class Point implements Serializable {
private float mX;
private float mY;
public Point() {
}
public Point(float x,float y) {
mX = x;
mY = y;
}
public float getX() {
return mX;
}
public float getY() {
return mY;
}
public void setX(float x) {
mX = x;
}
public void setY(float y) {
mY = y;
}
}
5、下载地址:https://files.cnblogs.com/liqw/Bezier.zip
本文来源于:http://www.cnblogs.com/liqw/p/3631137.html
有问题,请提问,大家一起研究!
关于Android日常学习:OpenGL 实践之贝塞尔曲线绘制和opengl贝塞尔曲面的介绍现已完结,谢谢您的耐心阅读,如果想了解更多关于Android Flutter利用贝塞尔曲线画一个小海豚、Android Path绘制贝塞尔曲线实现QQ拖拽泡泡、Android 之二阶贝塞尔曲线的波浪头像 (三阶的爱心飞出)、Android 贝塞尔曲线 折线图的相关知识,请在本站寻找。
本文标签:



![[转帖]Ubuntu 安装 Wine方法(ubuntu如何安装wine)](https://www.gvkun.com/zb_users/cache/thumbs/4c83df0e2303284d68480d1b1378581d-180-120-1.jpg)

