• 更改FloodFill-Algorithm以获得两个数据点的Voronoi领土？
• A Benchmark Comparsion of Monocular Visual-Inertial Odometry Algorithms for Flying Robots论文笔记
• Algorithm - Network Flow
• Algorithm - Network Flow 复习
• Algorithms 普林斯顿知识点熟记 - Analysis of Algorithms

更改FloodFill-Algorithm以获得两个数据点的Voronoi领土？

我得到了两分的网格。我想计算每个点可以到达的平方数。目前，我实现了FloodFill-Algoritm，它可以计算一个点可以达到的正方形数量。

如何更改该算法以同时或至少一个接一个地对两个点进行“泛洪”？

答案1

“每个点可以先到达另一个”是什么意思？

在我看来，您需要进行BF搜索。像这样使用FIFO队列：

令p1和p2为两点的位置。

令f为队列中的第一个元素，l为最后一个元素。最初，f = 0，l =1。令Q为队列。

Q[f] = p1Q[l] = p2while ( f <= l ){   poz = Q[f];   ++f;   for each neighbour poz'' of poz      if poz'' hasn''t been marked yet      {         mark poz''         add poz'' to Q: Q[++l] = poz      }}

Q将需要是网格的大小（行x列）。您可以使用两个矩阵：一个矩阵可以到达p1的位置，另一个可以到达p2的位置，或者可以使用一个矩阵并用正数标记正方形p1到达而负数标记正方形p2。如果您对他们在哪里相遇感兴趣，则只需要检查是否要从负值（poz负和poz的正）标记正值，或者反之亦然。基本上，这将依次进行泛洪：从p1泛洪一个平方，然后从p2泛洪，再从p1泛洪，再从p2泛洪，依此类推。

A Benchmark Comparsion of Monocular Visual-Inertial Odometry Algorithms for Flying Robots论文笔记

摘要：

　　本文主要比较单目VIO的算法在飞行机器人上运行的性能，测试使用统一数据集为EuRoC。其中评价指标为：姿态估计精度、每帧处理时间以及CPU和内存负载使用率，同时还有RMSE（运行轨迹与真实轨迹的比较指标）。比较的单目VIO分别为：MSCKF、OKVIS、ROVIO、VINS-Mono、SVO-MSF、SVO-GTSAM。其中运用了四个测试平台Intel NUC（desktop PC）、laptop、UP Board（embedded system for flying robots）、ODROID（an embedded PC containing a hybrid processing unit）

介绍：

　　选择单目的原因是由于单目是可靠状态估计所需的最小单元，而且相对于其他传感器而言，单目更加适合飞行机器人的负载和功耗需求，所以文章选择比较单目的VIO。因为各个单目VIO算法的性能比较都不全面，而且它们都没考虑计算能力限制的需求，所以本文将它们统一起来一起比较。

　　贡献：

　　　　1、全面比较了公开的单目VIO算法

　　　　2、提供比较结果的性能

算法介绍：

　　1）MSCKF（Multi-state constraint Kalman Filter）主要特点是提出一个测量模型，该模型描述了观察到特定图像特征的所有摄像机帧的姿态之间的几何约束，而不需要维持对该时刻3维特征位置的估计。扩展卡尔曼滤波后端实现了基于事件的相机输入的MSCKF形式，后面改为标准的相机追踪模式。

　　2）OKVIS（Open Keyframe-based Visual-Inertial SLAM）提出基于关键帧处理的思想，对包括关键帧位姿的一个滑动窗口进行非线性优化。文中提出一个基于视觉路标加权的投影误差和加权的惯性误差项组成的代价函数。前端使用多尺度Harris角点检测和提取BRISK描述子，后端使用ceres进行非线性优化。

　　3）ROVIO（Robust Visual Inertial Odometry）基于EKF的slam算法。提取Fast角特征，以机器人为中心的方位向量和距离参数化3D位姿，从围绕这些特征的图像流中摄取多层次的patch特征。在状态更新中提出光度误差项。

　　4）VINS-Mono提出基于滑动窗口的非线性优化估计器，前端追踪鲁棒的角特征。提出一种松耦合的传感器数据融合的初始化过程，可以从任意的状态下引导估计量。IMU测量在优化之前先预积分，提出紧耦合的优化方法。提出4自由度的优化位姿图和回环检测线程。

　　5）SVO+MSF（Semi-Direct Visual Odometry）MSF是在状态估计中融合不同传感器的通用EKF框架。SVO估计的位姿提供给MSF作为通用的位姿传感器输出，然后使用MSF融合IMU数据。由于松耦合的数据结合，姿态的尺度必须近似正确，需要手动设置初始化的值。

　　6）SVO+GTSAM后端使用iSAM2中执行在线因子图全平滑优化算法，在位姿图优化中提出使用预积分的IMU因子。

结论：

　　通过额外计算能力可以提高准确性和健壮性，但是在资源受限系统中，需要在计算能力和性能之间找到合适的平衡。在计算能力受限的系统中，ODROID、SVO+MSF算法性能最好，但是牺牲了精度，得出的鲁棒的轨迹；在计算能力不受限的系统中，VINS-Mono显示高精度和很好的鲁棒性。两者折中方案是ROVIO，比ODROID、SVO+MSF有更好的精度，且比VINS-Mono计算需求低。但是ROVIO对每帧处理时间敏感，无法在一些飞行机器人机载系统上使用。

Algorithm - Network Flow

OSC 请你来轰趴啦！1028 苏州源创会，一起寻宝 AI 时代

1. 判断题一道

2. 然后是这道超赞的题

这道题其实分成了好几道小题，其实是在间接引导你解题：

1. 如果告诉你这个 maze (graph) 就是一条直线 O->O->O->...->O，且每条边的 capacity 是 1，请问让所有人员都走出迷宫需要几晚上？

2. 假设现在有个函数 magic（k），能验证所有人能不能用少于 k 晚的时间走出迷宫（返回 boolean value），请问你要怎样利用这个函数去求出所有人到底要用几晚上走出迷宫。

3. 试着自己写出这个 magic（k）函数。

你看，这样一步一步引导下来，你其实就逐渐把这个问题解决了，真的很值得学习呢！

首先看第一步：显然，由于边的 capacity 是 1，每晚只能挪动一个人，所以总时长为 | V|+m-2，不要误以为是 | V|m 哦！

然后第二步：有了 magic（k），而我们在第一步已经知道，k 的可能范围是 <=|V|+m-2 的，所以只需要在 [0, |V|+m-2] 的范围内 binary search 找到能让 magic（k）返回 true 的最大 k 值就 ok 了。

时间复杂度为 O (TC (magic)*log (|V|+m-2))，其中 TC (magic) 为 magic（k）的 time complexity。

然后是第三步，最关键最难的啦，使用 network flow 把 magic (k) 实现：

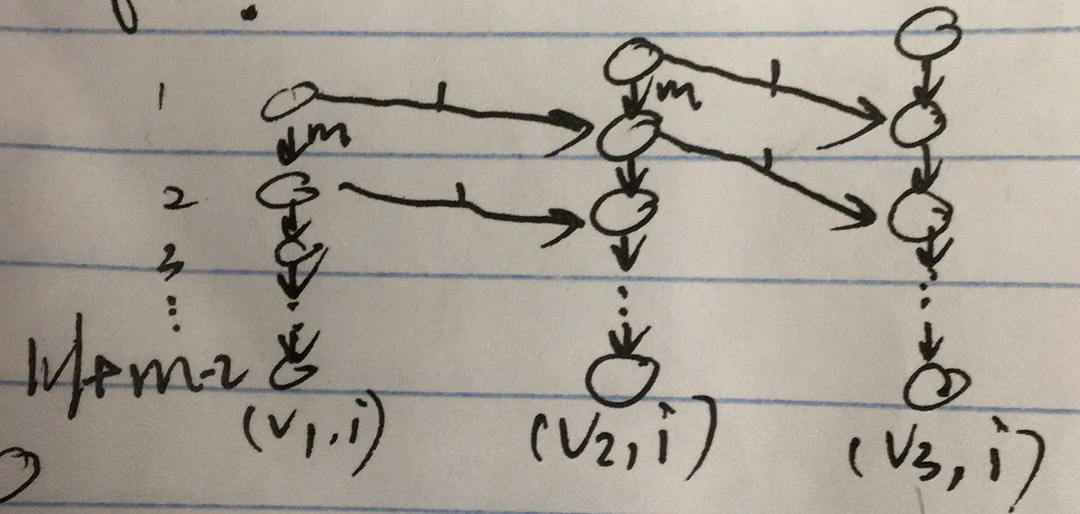
按照这样的方式完成构建 flow network，此时总时间限制为 k 晚。

1. 对每个原图中的 node-v 我们都复制 | V|+m-2 份，记为 (node-v, 1),(node-v, 2),(node-v, 3),...,(node-v, k)，并用 capacity 为 m 的边将他们连接起来。

    解释：同一个点复制 k 份是代表这个人在这个点停留到了 k 天，因为一共只有最晚会有人在第 k 天走出 graph，所以复制 k 份。而同一个点同时可以容纳的人数没有限制，所以这里的边的 capacity 应该是正无穷，表示第 i 晚呆在点 v 的人，在下一晚可以全部留下来，但因为反正一共才 m 个人，所以我这里就将 capacity 设为了 m。

2. 如果原图中的两 node，比如 n1 和 n2，之间存在边（n1,n2）的话，在这个新建图中就把每个（n1, i）和（n2, i+1）都连接起来，并且将该边的 capacity 设为 1

    解释：边 <(n1, i), (n2, i+1)> 表示在第 i 晚可以有一个人从一点走到下一点。

完成这个 flow network 后对这个图进行 fordfulkerson 算法，source 点设为（node-0, 0）, sink 点设为（node-n, k），求得 maxflow，如果这个 maxflow 小于人数 m，那就 return false；反之 return true。

Algorithm - Network Flow 复习

network flow 的应用：

1. bipartite matching problem。（employee 和 job 的分配匹配问题）

    - 构建 bipartite 图，添加 s,t。

    - 看问题中变量的意义，决定图中各边的 capacity。（有点玄学）

    - 算 max flow，用 ford-fulkerson 或者别的什么 max flow 算法。

2. minimum cut problem。（image segmentation 问题）

    - 利用的是 minimum cut = max flow

--------------------------------------------------------------------------

ford-fulkerson 算法伪码：

Ford-Fulkerson  
  
    for <u,v> ∈ E  
  
        <u,v>.f = 0  
  
    while find a route from s to t in e  
  
        m = min(<u,v>.f, <u,v>  ∈ route)  
  
        for <u,v> ∈ route  
  
            if <u,v>  ∈ f  
  
                <u,v>.f = <u,v>.f + m  
  
            else  
  
                <v,u>.f = <v,u>.f - m 

cut（割）的容量（设 cut<S,T>）= 所有从 S 到 T 的 edge 的 capacity 的和

cut 的 flow = 所有从 S 到 T 的 edge 上的 flow - 所有从 T 到 S 的 edge 上的 flow

如何证明 ford-fulkerson 能得到 max flow？（如何证明没有 augmented path 的时候就达到 max flow 了）

证明：将 residual graph 里所有所有源点 s 能 reach 到的 node 看作集合 S，那么所有 node 的集合 V 减去集合 S 就是集合 T=V-S，T 就是所有源点 s 无法 reach 到的点，此时（S，T）就是一个割。那么对于所有跨 cut<S,T> 的边 < u,v > 必然有 flow（<u,v>）=capacity (<u,v>)，不然的话就说明在 residual graph 中 u 有路径可以连接到 v，也就是说源点 s 可以 reach 到 T 中的 v，这和 T 的定义矛盾。

MIT quiz 题：（network flow 是）

https://ocw.mit.edu/courses/electrical-engineering-and-computer-science/6-046j-design-and-analysis-of-algorithms-spring-2015/exams/MIT6_046JS15_quiz2sols.pdf

Algorithms 普林斯顿知识点熟记 - Analysis of Algorithms

为什么需要分析算法？

1. 对性能进行预测
2. 进行算法比较
3. 为结果提供保障
4. 理解理论基础

双对数（以2为底）坐标作图，横坐标是数据量的对数，纵坐标是运行时间的对数，得到的斜率 k 的值意味着 数据量每增加一倍，所要花费的时间大约是之前运行时间的2^k倍。比如斜率为3,1k用时为1s，那么2k用时就为1*2^3 s = 8 s

幂定律

a 取决于电脑本身的硬件和软件等
b 取决于算法

数学模型

计算如下代码片段数组的访问次数

int sum = 0;
for (int i = 0; i < n; i++)
    for (int j = i+1; j < n; j++)
        for (int k = 1; k < n; k = k*2)
            if (a[i] + a[j] >= a[k]) sum++;

前面两个循环共执行如下次数

第三个循环中，k 的值依次是

注：

故第三个循环共执行如下次数：

所以整个数组的访问次数 = 前两个循环的循环次数 * 第三个循环的次数 * 每次循环访问数组的次数

增长阶数

二叉搜索分析

public static int binarySearch(int[] a, int key)
{
    int lo = 0, hi = a.length-1; 
    while (lo <= hi) {
        int mid = lo + (hi - lo) / 2;
        if (key < a[mid]) hi = mid - 1;
        else if (key > a[mid]) lo = mid + 1;
        else return mid; 
    } 
    return -1; 
}

优化后的 3-sum 算法（复杂度为 N^2 logN）

Theory of Algorithms

O 增长阶数的上界
Ω 增长阶数的下界
Θ 增长阶数的上下界

关于 Which of the following function is O(n^3) ?
该问题为什么全选，coursera的导师Beau Dobbin是这样回答的

Getting familiar with Big "O" notation takes a little while. The key to remember is that Big "O" defines an upper bound for a growth rate. It can seem confusing that such different functions have the same Big "O" _order_.

In other words, as all three functions approach infinite, they are all less than or equal to "n^3". You could also say that all three are O(n^789457398). As long as the Big "O" function grows faster (or equal), the notation holds.

Similarly, Big Omega "Ω" and Theta "Ө" notations represent lower bounds and _simultaneous upper and lower bounds_.

In other words:

If your algorithm "runs in O(n^2) time", it takes at most (n^2) time.

If your algorithm "runs in Ω(n^2) time", it takes at least (n^2) time.

If your algorithm "runs in Ө(n^2) time", it takes at most (n^2) time and at least (n^2) time. This is similar to saying "it runs in exactly (n^2) time," but it''s not exact. It''s the asymptotic time as n approaches infinite.

https://en.wikipedia.org/wiki/Big_O_notation : Look for "A description of a function in terms of big O notation usually only provides an upper bound on the growth rate of the function."[](https://www.desmos.com/calcul...

[](https://en.wikipedia.org/wiki...https://en.wikipedia.org/wiki/Big_O_notation#Family_of_Bachmann.E2.80.93Landau_notations : A comparison of a few common notations.

https://www.desmos.com/calculator/7vmsklh8o9 : A graph of the three functions.

memory

• Object overhead. 16 bytes.
• Reference. 8 bytes.
• Padding. Each object uses a multiple of 8 bytes

今天关于更改FloodFill-Algorithm以获得两个数据点的Voronoi领土？的分享就到这里，希望大家有所收获，若想了解更多关于A Benchmark Comparsion of Monocular Visual-Inertial Odometry Algorithms for Flying Robots论文笔记、Algorithm - Network Flow、Algorithm - Network Flow 复习、Algorithms 普林斯顿知识点熟记 - Analysis of Algorithms等相关知识，可以在本站进行查询。