对于jsworker效果对比斐波那契数列计算感兴趣的读者,本文将会是一篇不错的选择,我们将详细介绍js实现斐波那契数列,并为您提供关于2.生成器计算出斐波那契数列、9.斐波那契数列、JS从斐波那契数列
对于js worker 效果 对比 斐波那契数列计算感兴趣的读者,本文将会是一篇不错的选择,我们将详细介绍js实现斐波那契数列,并为您提供关于2.生成器计算出斐波那契数列、9. 斐波那契数列、JS 从斐波那契数列浅谈递归、JS 函数实现和递归实现斐波那契数列 || js 两种方法实现斐波那契数列的有用信息。
本文目录一览:- js worker 效果 对比 斐波那契数列计算(js实现斐波那契数列)
- 2.生成器计算出斐波那契数列
- 9. 斐波那契数列
- JS 从斐波那契数列浅谈递归
- JS 函数实现和递归实现斐波那契数列 || js 两种方法实现斐波那契数列

js worker 效果 对比 斐波那契数列计算(js实现斐波那契数列)
原文链接: js worker 效果 对比 斐波那契数列计算
上一篇: JS 的深拷贝/浅拷贝
下一篇: Electron 简单使用
普通版, 进行大量计算时, 主线程会卡顿, 用户将无法进行dom操作, 浏览器假死
<!DOCTYPE html>
<html lang="en">
<head>
<meta charset="UTF-8">
<title>Title</title>
</head>
<body>
<h1>worker</h1>
<input type="number" id="value">
<button id="btn">click</button>
<h3 id="res"></h3>
<script>
function fib(n) {
return n < 2 ? n : fib(n - 1) + fib(n - 2)
}
let worker = new Worker(''worker.js'');
document.getElementById(''btn'').addEventListener(
''click'', () => {
let n = document.getElementById(''value'').value
console.log(n)
worker.postMessage(n);
worker.onmessage = function (event) {
console.log(''Received message '' + event.data);
document.getElementById(''res'').innerText = event.data
}
}
)
</script>
</body>
</html>
worker
在进行大量计算时, dom依然可以操作, 虽然结果会有延迟显示, 但可以使用loading等ui告知用户
不会出现浏览器假死的情况
html
<!DOCTYPE html>
<html lang="en">
<head>
<meta charset="UTF-8">
<title>Title</title>
</head>
<body>
<h1>worker</h1>
<input type="number" id="value">
<button id="btn">click</button>
<h3 id="res"></h3>
<script>
let worker = new Worker(''worker.js'');
document.getElementById(''btn'').addEventListener(
''click'', () => {
let n = document.getElementById(''value'').value
console.log(n)
worker.postMessage(n);
worker.onmessage = function (event) {
console.log(''Received message '' + event.data);
document.getElementById(''res'').innerText = event.data
}
}
)
</script>
</body>
</html>
worker.js
addEventListener(''message'', function (e) {
let st = new Date().getTime()
let res = fib(e.data)
let ed = new Date().getTime()
console.log(ed - st)
self.postMessage(res);
}, false);
function fib(n) {
return n < 2 ? n : fib(n - 1) + fib(n - 2)
}

2.生成器计算出斐波那契数列
#斐波那契数列:1,1,2,3,5,8,13...
def fib(times):
a = 0
b = 1
n = 1
while n <= times:
# print(b)
#返回加到F生成器中,每次都叠加
yield b
a,b = b,a+b
n += 1
return ''done''
F = fib(10)
# 获取生成器函数返回值,用捕获StopIteration异常
while True:
try:
print(next(F))
except StopIteration as e:
print(e.value)
break
''''''
总结:
生成器它能返回记住上一次返回时函数体中的位置,对生成器函数的第二次(或第n次),
调用跳转至函数中间yield处,而上次调用的所有的局部变量都保持不变
生成器不仅"记住"数据状态,还记住了它在流程控制构造中的位置
生成器的特点:
1.节约内存
2.保存(上一次的)状态
''''''
# print(next(F))
# print(next(F))
# print(next(F))
# print(next(F))#在异常后面显示返回值
# F = fib(7) #F是一个生成器
# print(F)
# for i in F:
# print(i)
''''''
yield的作用就把一个函数变成一个生成器,带有yield函数不再是一个普通函数
python解释器会将其视为一个生成器generator,调用fib(7)不会执行fib函数
而是返回一个迭代器对象,在for循环执行时,每次循环都会执行fib函数内部的代码
执行到yield b时,fib函数就返回一个值.下次再调用的时候,其实代码接着由中断代码
接着执行
''''''

9. 斐波那契数列
题目:写一个函数,输入n,求斐波那契(Fibonacci)数列的第n项。斐波那契数列的定义如下:
{ 0 n = 0
f(n) = { 1 n = 1
{ f(n-1) + f(n-2) n > 1
思路:
1.传统递归算法:从上至下,也就是算f(5)的时候算f(4)和f(3),以及类推。然后这样会导致重复操作,f(5)得算f(4)和f(3),f(4)得算f(3)和f(2),这样f(3)就重复计算。
2.改进循环算法:从下至上计算,保存中间值,直接进入下一环节的计算,而不是重新计算。从下层往上层递增。
测试用例:
1.功能测试(如输入3、5、10等)
2.边界值测试(如输入0、1、2)。
3.性能测试(输入较大的数字,如40、50、100等)
传统递归算法:
#include<iostream>
#include<cstdio>
using namespace std;
long long Fibonacci(unsigned int n)
{
if (n <= 0)
{
return 0;
}
if (n == 1)
{
return 1;
}
return Fibonacci(n - 1) + Fibonacci(n - 2);
}
//测试
void test1()
{
long long result = Fibonacci(10);
cout << result << endl;
}
void test2()
{
long long result1 = Fibonacci(0);
long long result2 = Fibonacci(1);
long long result3 = Fibonacci(2);
cout << result1 << " " << result2 << " " << result3 << endl;
}
void test3()
{
long long result = Fibonacci(50);
cout << result << endl;
}
int main()
{
test1();
test2();
test3();
return 0;
}
改进循环算法:
#include<iostream>
#include<cstdio>
using namespace std;
long long Fibonacci(unsigned n)
{
int result[2] = {0, 1};
if (n < 2)
{
return result[n];
}
long long fibMinOne = 1;
long long fibMinTwo = 0;
long long fibN = 0;
for (unsigned int i = 2; i <= n; i++)
{
fibN = fibMinOne + fibMinTwo;
fibMinTwo = fibMinOne;
fibMinOne = fibN;
}
return fibN;
}
//测试
void test1()
{
long long result = Fibonacci(10);
cout << result << endl;
}
void test2()
{
long long result1 = Fibonacci(0);
long long result2 = Fibonacci(1);
long long result3 = Fibonacci(2);
cout << result1 << " " << result2 << " " << result3 << endl;
}
void test3()
{
long long result = Fibonacci(500);
cout << result << endl;
}
int main()
{
test1();
test2();
test3();
return 0;
}
运行的时候,传统递归输入50就已经跑不动了,而改进循环的那个算法输入500一下子就跑出来了。

JS 从斐波那契数列浅谈递归
一、前言
昨晚下班后,经理出于兴趣给我们技术组讲了讲算法相关的东西,全程一脸懵逼的听,中途还给我们出了一道比较有趣的爬楼问题,问题如下:
假设一个人从地面开始爬楼梯,规定一步只能爬一坎或者两坎,人只能往上走,例如爬到第一坎,很明显从地面到第一坎只有一种可选方式,从地面爬到第二坎,他可以从地面直接跨到第二坎,也可以先从地面到第一坎,再从第一坎到第二坎,也就是2种可选方式,那么求他爬到N楼一共有几种可选方式。
这道题涉及到了斐波那契数列,要求使用递归来求值,技术贼菜的我也是一脸懵逼,所以本着学习的心还是记录下来了。
二、有趣的斐波那契数列
我们将地面理解为数字0,第一坎理解为数字1,以此来进行简单的分析:
例如从0到1,就一种选择,如图(公司不让用破解软件,没PS画图,凑合看吧,画图的手微微颤抖。。。)
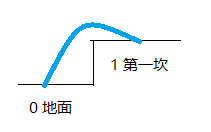
那么,现在要求到第二坎,从0到2呢,两种选择,看图分析(记住,一步只能跨一坎或者两坎):
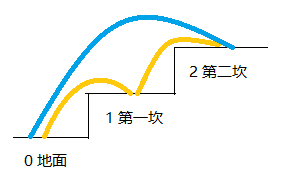
当要求从0到3,三种选择,如图:

紫色:一坎坎的走;黄色:先走两坎,再走一坎;蓝色:先走一坎,再走两坎。
从0-4,一共五种情况,如图:
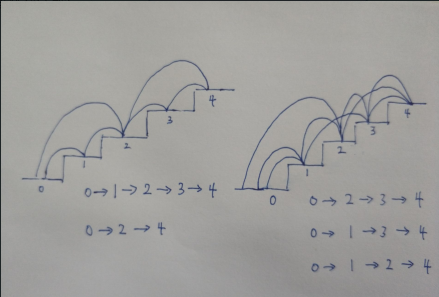
这里我分开画了,左边的2种情况加上右边的三种情况
左边:
第一种:一坎坎的走,0-1-2-3-4
第二种:两坎两坎走,0-2-4
右边:
第三种:先走两坎,再一坎坎的走0-2-3-4
第四种:先走一坎,再走两坎,再走一坎0-1-3-4
第五种:先走一坎,再走一坎,再走两坎0-1-2-4
当我们继续往后画,楼梯层对应走法会形成一个有趣的规律,
从第三层开始,第三层的走法等于一层与二层走法的和,第四层的走法等于第二层和第三层走法的和.....针对楼梯问题,我们可以得到如下公式:
F(n) = F(n-1) + F(n-2) n>=3
这就是著名的斐波那契数列(Fibonacci sequence),又称黄金分割数列。有兴趣的同学可以查查兔子繁殖问题。

百科里斐波那契数列的基数n>=4是根据实际情况来定的,这点不用纠结。
三、斐波那契数列与递归的结合
什么是递归?自己调用自己的函数就是递归,这么说完全没问题。
我们回归上面的问题,要求第N层的走法,那我们只需要知道N-1层和N-2层的走法就好了,假设N是10,求到第十层的走法。
十层走法=九层的走法+八层走法
九层和八层也可以拆分啊,九层走法 = 七层走法 + 八层走法 ,而八层走法 = 七层走法 + 六层走法
.......
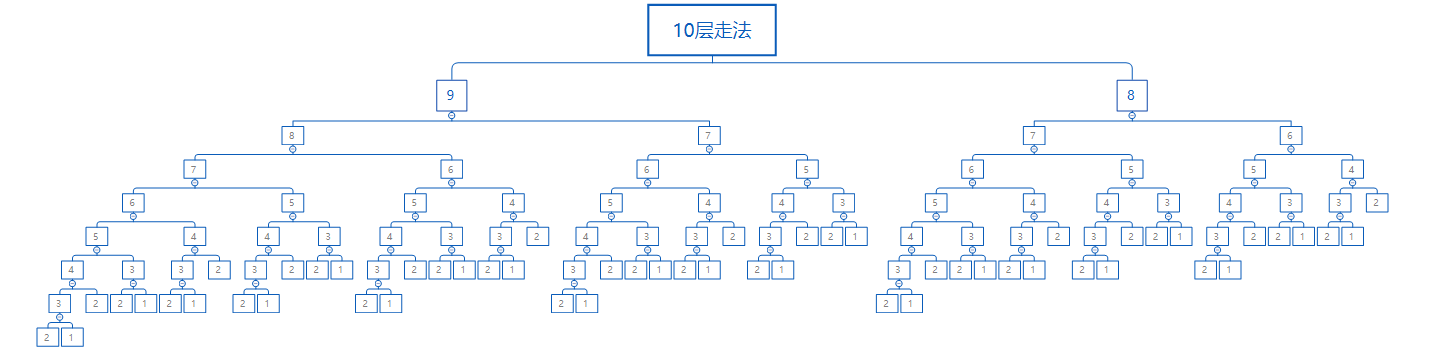
当分到3层时,最后还可以拆分为1层+2层,因为规律是从第三层开始的,因为此公式不适用于1层和2层,分到1层和2层就代表分支的结束了。
使用闭包需要找到跳出自己调用自己的的临界条件,不然会会陷入死循环,那对应我们的楼梯问题,只要N<3时就不需要继续调用自己了,因为不需要继续产生分支了。
这个闭包怎么写呢?我们结合斐波那契数列公式尝试一下吧。
现在有一个函数,里面申明一个走法变量var step = 0;输入一个数字N,我们会对N判断,只要N>=3,它就会自己调用自己,小于3时,我们分别判断它等于1或者2,等于1就让step加1,等于2就让step加2,如下:
function recursion(n){
let step = 0;
if (n === 1 ){
step += 1
}else if (n === 2){
step += 2;
}else if (n >= 3){
step = recursion(n-1) + recursion(n-2);
};
return step;
};
console.log(recursion(10))//89种为了验证,我将上方分支图中所有的1与2相加(1层只有1种走法,2层有2种),得出数字也确实是89。所以我不明白我为什么要把基数N设置为10,算的难受。
那么趁热打铁,活学活用,现在我们尝试求正整数N与N之前所有正整数累加的和。
例如3之前累加的和就是3+2+1,数字0加不加没意义,所以跳出递归的临界条件就是当N>=2时,最后调用一次让之前数字的和加一次1就好了。
var result = 0;
function add(n){
result += n
n>=2 ? add(n-1) : null;
return result;
};
console.log(add(10));//55验证一下,完全没问题,有没有觉得递归挺简单。
当你看到这时,恭喜你,不仅了解了斐波那契数列,也简单了解了递归的用法。其实本人在工作中需要操作数据,本能的总是想到穷举,循环,那么现在又多了一种可行的解决方法,也算是对于思维的开拓了。
留个问题,回到上方两段实现代码,为什么第一个变量申明在函数体内,而第二个数字累加的变量申明要在函数体外呢?尝试思考下。
当然,前提是,这篇博客如果有人愿意看完就挺好了。


JS 函数实现和递归实现斐波那契数列 || js 两种方法实现斐波那契数列
斐波那契数列作为程序员的必备知识点,初学者更应当深入理解与掌握。斐波那契数列由 1 和 1 开始,之后的斐波那契数列系数就由之前的两数相加。js 函数实现斐波那契数列代码如下:
函数实现:
1 <script type="text/javascript">
2 function fibonacci(n) {
3 var one = 1;
4 var two = 1;
5 for(var i = 3; i <= n; i++) { //此处代码重点部分,用three累加前两个数的和,也是斐波那契数列的精髓所在。
6 var three = one + two;
7 one = two;
8 two = three;
9
10 }
11 if (n==1||n==2) { //判断n==1或2的情况下返回undefined
12 return one;
13 }
14 return three; //最后返回three
15 }
16 console.log(fibonacci(2));
17 </script>递归实现:
1 function box(m){
2 if(m==1||m==2){
3 return 1;
4 }
5 8 return box(m-1)+box(m-2); //除去1和2的两种情况,递归斐波那契数列一行代码就能搞定,但是递归性能是大大不如函数的。
9 }
10 alert(box(2));
今天关于js worker 效果 对比 斐波那契数列计算和js实现斐波那契数列的介绍到此结束,谢谢您的阅读,有关2.生成器计算出斐波那契数列、9. 斐波那契数列、JS 从斐波那契数列浅谈递归、JS 函数实现和递归实现斐波那契数列 || js 两种方法实现斐波那契数列等更多相关知识的信息可以在本站进行查询。
本文标签:



![[转帖]Ubuntu 安装 Wine方法(ubuntu如何安装wine)](https://www.gvkun.com/zb_users/cache/thumbs/4c83df0e2303284d68480d1b1378581d-180-120-1.jpg)

