#include <stdio.h>
#include <string.h>
#include <math.h>
#include <algorithm>
using namespace std;
int c[10001];//记录最大因子个数
int d[10001],m;//记录大数和数长
void mul(int t)//大数乘法
{
    int i,j,k,temp=0;
    for(i=0;i<m;i++)
        d[i]*=t;
    for(i=0;i<m;i++)
    {
        k=d[i]+temp;
        temp=k/10;
        d[i]=k%10;
    }
    while(temp)
    {
        d[m]=temp%10;
        temp=temp/10;
        m++;
    }
}
int main()
{
    int T,tt=0;
    scanf("%d",&T);
    while(T--)
    {
        memset(c,sizeof(c));
        memset(d,sizeof(d));
        int n,i,t;
        scanf("%d",&n);
        while(n--)
        {
            scanf("%d",&t);
            i=2;
            while(t!=1)
            {
                k=0;
                if(t%i==0)
                {
                    t=t/i;
                    k++;
                    while(t%i==0){t=t/i;k++;}
                }
                c[i]=max(c[i],k);
                i++;
            }
        }
        d[0]=m=1;
        for(i=2;i<10000;i++)
        {
            if(c[i]==0)
                continue;
            t=(int)pow(i,c[i]);
            //printf("%d\n",t);
            mul(t);
        }
        printf("Case %d: ",++tt);
        for(i=m-1;i>=0;i--)
            printf("%d",d[i]);
        printf("\n");
    }
    return 0;
}
/*
题意：输入一堆数，求这堆数的最小公倍数。
将每个数因式分解，用一个数组记录各个数的因子，因子数保存最大值。最后将所有因子乘起来就是最小公倍数
*/

本文分享自微信公众号 - 福大大架构师每日一题（gh_bbe96e5def84）。
如有侵权，请联系 support@oschina.cn 删除。
本文参与“OSC源创计划”，欢迎正在阅读的你也加入，一起分享。

2020-09-22：已知两个数的最大公约数和最小公倍数，并且这两个数不能是最大公约数和最小公倍数本身。如何判断这两个数是否存在？

福哥答案2020-09-22：#福大大架构师每日一题#

1.如果最小公倍数不能被最大公约数整除，不存在这两个数。
2.求【商】=【最小公倍数/最大公约数】。
3.判断【商】是否是质数，如果是，直接返回false。这个步骤可以不要。
4.幂次方缩小【商】范围，如果【商】是a的b次方，【商】变成a。
5.判断【商】是否是质数，如果是，直接返回false。
6.经过所有考验，返回true。

代码用python语言编写。代码如下：

# -*-coding:utf-8-*-

import math


# 求快速幂。ret = a^b%p。
def quick_power(a, b, p):
    """ 求快速幂。ret = a^b%p。 Args: a: 底数。大于等于0并且是整数。 b: 指数。大于等于0并且是整数。 p: 模数。大于0并且是整数。 Returns: 返回结果。 Raises: IOError: 无错误。 """
    a = a % p
    ans = 1
    while b != 0:
        if b & 1:
            ans = (ans * a) % p
        b >>= 1
        a = (a * a) % p
    return ans


# 求num的exp开方,exp是指数，num是结果。求底数。
def _get_sqrt_range(num, right, exp=2):
    """ 求num的exp开方,exp是指数，num是结果。求底数。 Args: num: 大于等于0并且是整数。 right: 大于等于0并且是整数。右边界。 exp: 大于等于0并且是整数。 Returns: 返回元组，表示一个开方范围。 Raises: IOError: 无错误。 """
    left = 1
    if num == 0:
        return 0, 0
    if num == 1:
        return 1, 1
    if num == 2 or num == 3:
        return 1, 2
    while True:
        mid = (left + right) // 2
        if mid ** exp > num:
            right = mid
            if left ** exp == num:
                return left, left
            if left + 1 == right:
                return left, right
        elif mid ** exp < num:
            left = mid
            if right ** exp == num:
                return right, right
            if left + 1 == right:
                return left, right
            if mid == 1:
                return 1, 2
        else:
            return mid, mid


# 求对数范围
def get_log_range(num, basenum):
    """ 求对数范围。 Args: num: 数，大于等于1并且是整数。 basenum: 底数，大于等于2并且是整数。 Returns: 返回结果。对数范围。 Raises: IOError: 无错误。 """
    if num == 1:
        return 0, 0
    else:
        n = 0
        ism = 0
        while num >= basenum:
            if ism == 0 and num % basenum != 0:
                ism = 1
            n += 1
            num //= basenum
        return n, n + ism


# 判断幂次方，并且返回底数
def is_power2(num):
    """ 判断n是否是一个数的幂次方形式。 Args: num: 大于等于0并且是整数。 Returns: 返回结果。true是幂数 Raises: IOError: 无错误。 """
    if num <= 3:
        return False, 0
    else:
        log_range = get_log_range(num, 2)
        if log_range[0] == log_range[1]:
            return True, 2
        expmax = log_range[0]
        expmin = 2
        exp = expmin
        sqrt = 0
        right = 2 ** (1 + log_range[0] // 2)
        while exp <= expmax:
            sqrt = _get_sqrt_range(num, right, exp)
            right = sqrt[0]  # 缩小右边界范围
            if sqrt[0] == sqrt[1]:
                return True, sqrt[0]
            if sqrt == (1, 2):
                return False, 0
            exp += 1
        return False, 0


# 米勒-拉宾素性检验是一种概率算法，但是，Jim Sinclair发现了一组数：2, 325, 9375, 28178, 450775, 9780504, 1795265022。用它们做 [公式] ， [公式] 以内不会出错，我们使用这组数，就不用担心运气太差了。
def is_prime_miller_rabin(num):
    """ 判断是否是素数。米勒拉宾素性检验是一种概率算法 可能会把合数误判为质数。 Args: num: 大于等于2并且是整数。 Returns: 返回结果。true为素数；false是非素数。 Raises: IOError: 无错误。 """
    # num=(2^s)*t
    a = 2  # 2, 325, 9375, 28178, 450775, 9780504, 1795265022
    s = 0
    t = num - 1
    num_1 = t
    if num == 2:
        return True
    if not (num % 2):
        return False
    while not (t & 1):
        t >>= 1
        s += 1
    k = quick_power(a, t, num)
    if k == 1:
        return True
    j = 0
    while j < s:
        if k == num_1:
            return True
        j += 1
        k = k * k % num
    return False


# 综合法
def is_prime_comprehensive(num):
    """ 判断是否是素数。综合算法:试除法+米勒拉宾素性检验 可能会把合数误判为质数。 Args: num: 大于等于2并且是整数。 Returns: 返回结果。true为素数；false是非素数。 Raises: IOError: 无错误。 """
    if num <= 1:
        return False
    if num == 2:
        return True
    if num & 1 == 0:
        return False

    # 100以内的质数表
    primeList = [3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97]

    # 质数表是否能整除
    for prime in primeList:
        if num == prime:
            return True
        if num % prime:
            if prime * prime >= num:
                return True
        else:
            return False

    # 米勒拉宾素性检验
    return is_prime_miller_rabin(num)


# 已知两个数的最大公约数和最小公倍数，并且这两个数不能是最大公约数和最小公倍数本身。如何判断这两个数是否存在？
def is_exist_two_nums_by_gcd_lcm_not(gcd, lcm):
    """ 已知两个数的最大公约数和最小公倍数，并且这两个数不能是最大公约数和最小公倍数本身。如何判断这两个数是否存在？ Args: gcd: 大于等于1并且是整数。最大公约数。 lcm: 大于等于1并且是整数。最小公倍数。 Returns: 返回True，说明存在。 Raises: IOError: 无错误。 """
    # 1.如果最小公倍数不能被最大公约数整除，不存在这两个数。
    if lcm % gcd != 0:
        return False

    # 2.求【商】=【最小公倍数/最大公约数】。
    quotient = lcm // gcd

    # 3.判断【商】是否是质数，如果是，直接返回false。这个步骤可以不要。
    if is_prime_comprehensive(quotient):
        return False

    # 4.幂次方缩小【商】范围，如果【商】是a的b次方，【商】变成a。
    isloop = True
    quotienttemp = 0
    while isloop:
        isloop, quotienttemp = is_power2(quotient)
        if isloop:
            quotient = quotienttemp

    # 5.判断【商】是否是质数，如果是，直接返回false。
    if is_prime_comprehensive(quotient):
        return False

    # 6.经过所有考验，返回true。
    return True


if __name__ == "__main__":
    gcd = 5
    lcm = 35
    print("gcd = ", gcd, ",lcm = ", lcm, ",", is_exist_two_nums_by_gcd_lcm_not(gcd, lcm))
    gcd = 5
    lcm = 20
    print("gcd = ", gcd, ",lcm = ", lcm, ",", is_exist_two_nums_by_gcd_lcm_not(gcd, lcm))
    gcd = 3
    lcm = 60
    print("gcd = ", gcd, ",lcm = ", lcm, ",", is_exist_two_nums_by_gcd_lcm_not(gcd, lcm))

代码结果执行如下：

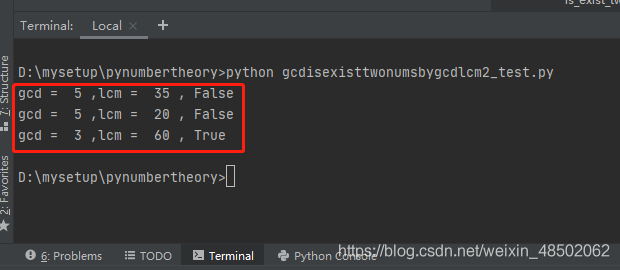
评论

C# 求俩个正整数的最小公倍数和最大公约数

C# 求俩个正整数的最小公倍数和最大公约数

1.公倍数、最小公倍数

两个或多个整数公有的倍数叫做它们的公倍数，其中除0以外最小的一个公倍数就叫做这几个整数的最小公倍数

翻开小学5年级下册PPT

1.1介绍

常用办法

1、列举法

   例如：求6和8的最小公倍数。

   6的倍数有：6，12，18，24，30，36，42，48，……

   8的倍数有：8，16，24，32，40，48，……

   6和8的公倍数：24，48，……其中24是6和8的最小公倍数。

   这种方法是先分别写出各自的倍数，再找出它们的公倍数，然后在公倍数里找出它们的最小公倍数。

2、分解质因数法。

   我们也可以利用分解质因数的方法，比较简便地求出两个数的最小公倍数。

   例如：求60和42的最小公倍数。

60=2×2×3×5   42=2×3×7

60和42的最小公倍数=2×3×2×5×7=420 。

这种方法是把60和42分别质因数后，观察相同的质因数只取一个（如2，3），把各自独有的质因数全部乘进去，所得的积就是这两个数的最小公倍数。

3、短除法。

  用短除法求18和24的最小公倍数。

2      18      24     …………先同时除以公因数2

    3   9      12    …………再同时除以公因数3

        3       4    ……除到两个商只有公因数1为止。

把所有的除数和最后的两个商连乘，得到：18和24的最小公倍数是2×3×3×4＝72，可表示为[18,24]＝2×3×3×4＝72。

用短除法求两个数的最小公倍数，一般都用这两个数除以它们的公因数，一直除到所得的两个商只有公因数1为止。把所有的除数和最后的两个商连乘起来，就得到这两个数的最小公倍数。

2.公约数、最大公约数

2.1介绍

公约数，亦称“公因数”。它是一个能被若干个整数同时均整除的整数。如果一个整数同时是几个整数的约数，称这个整数为它们的“公约数”；公约数中最大的称为最大公约数。

翻开小学5年级下册PPT 约数和公约数，最大公约数

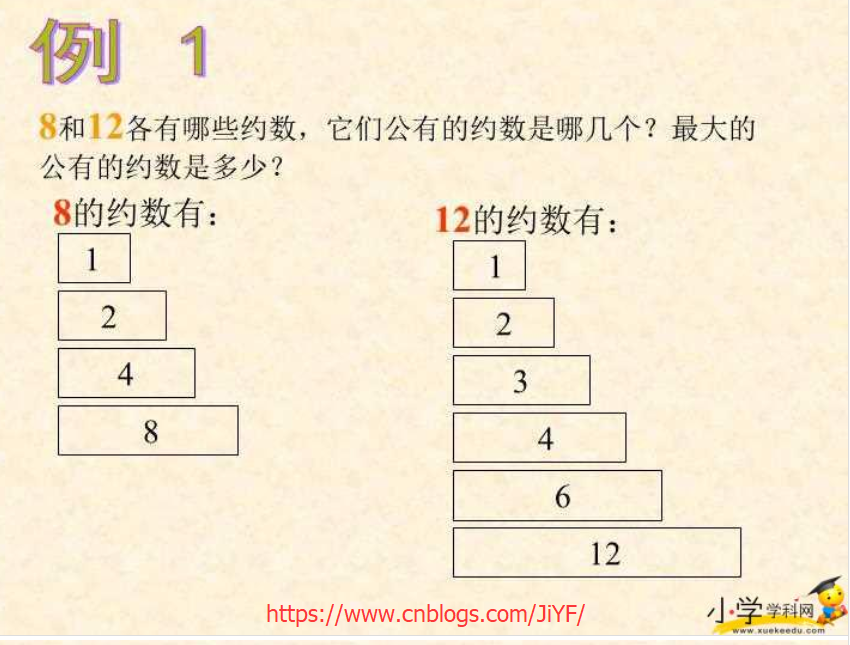
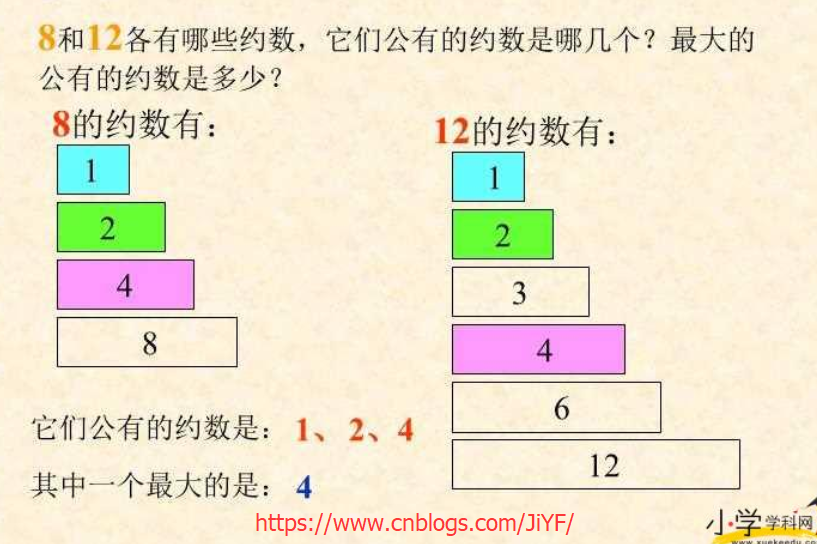
 2.2 最小公倍数和最大公约数关系

两个数的乘积等于这两个数的最大公约数与最小公倍数的乘积。

3.C#代码实现

代码：

 1     class Program
 2     {
 3         static void Main(string[] args)
 4         {
 5             int n = GetMinimumCommonMultiple(3, 5);
 6             System.Console.WriteLine("3,5最小公倍数为:" + n.ToString());
 7             n = GetMinimumCommonMultiple(2, 4);
 8             System.Console.WriteLine("2,4最小公倍数为:" + n.ToString());
 9 
10 
11             int numb = GetGreatestCommonDivisor(4, 8);
12             System.Console.WriteLine("4,8最大公约数为:" + numb.ToString());
13             numb = GetGreatestCommonDivisor(3, 15);
14             System.Console.WriteLine("3,15最大公约数为:" + numb.ToString());
15 
16 
17 
18             System.Console.Read();
19         }
20 
21 
22         /// <summary>
23         /// //最大公约数 
24         /// </summary>
25         static int GetGreatestCommonDivisor(int a, int b)
26         {
27             if (a < b)
28             {
29                 a = a + b;
30                 b = a - b;
31                 a = a - b;
32             }
33             return (a % b == 0) ? b : GetGreatestCommonDivisor(a % b, b);
34         }
35 
36         /// <summary>
37         /// //最小公倍数 
38         /// </summary>
39         static int GetMinimumCommonMultiple(int a, int b)
40         {
41             return a * b / GetGreatestCommonDivisor(a, b);
42         }
43     }

4.程序测试

C++ 实现求 N 个数的最大公约数和最小公倍数

算法实现：

#include <iostream>
using namespace std;

int divisor(int a,int b);
int ndivisor(int *a,int n);
int multiple(int a,int b);
int nmultiple(int *a,int b);

int main()
{
    cout<<"请选择计算的数据数量："<<endl;
    int n;
    cin>>n;
    while(cin.fail()){
        cout<<"Wrong, you have inputed a wrong type data\n"<<endl;
        cin.clear();//清除错误标记，重新打开输入流，但是输入流中依旧保留着之前的不匹配的类型
        /*cin.sync();*///清除cin缓存区的数据。
        while(cin.get() != ''\n''){
            continue;
        }
        cout<<"please input again"<<endl;
        cin>>n;
    }
    cout<<"请输入"<<n<<"个数据："<<endl;
    int a[n];
    for(int m=0;m<n;m++)
        cin>>a[m];
    int div=ndivisor(a,n);
    int mul=nmultiple(a,n);
    cout<<"上述"<<n<<"个数字的最大公约数为："<<div<<endl;
    cout<<"上述"<<n<<"个数字的最小公倍数为："<<mul<<endl;
    return 0;
}

int divisor(int a,int b)//两个数求最大公约数
{
    int temp;
    if(a<b)
    {
        temp=a;
        a=b;
        b=temp;
    }
    while(b!=0)
    {
        temp=a%b;
        a=b;
        b=temp;
    }
    return a;
}

int ndivisor(int *a,int n)//n个数求最大公约数
{
    if(n==1)
        return(*a);
    return divisor(a[n-1],ndivisor(a,n-1));
}

int multiple(int a,int b)//求最小公倍数
{
    int divisor(int a,int b);
    int temp=divisor(a,b);
    return(a*b/temp);
}


int nmultiple(int *a, int n)//求n个数的最小公倍数
{
    if (n == 1)
        return *a;
    else
        return multiple(a[n-1], nmultiple(a, n-1));
}

关于light 1024 Eid 大数除法+多个数的最小公倍数和多个数求最大公因数和最小公倍数的介绍现已完结，谢谢您的耐心阅读，如果想了解更多关于2020-09-22：已知两个数的最大公约数和最小公倍数，并且这两个数不能是最大公约数和最小公倍数本身。如何判断这两个数是否存在、2020-09-22：已知两个数的最大公约数和最小公倍数，并且这两个数不能是最大公约数和最小公倍数本身。如何判断这两个数是否存在？、C# 求俩个正整数的最小公倍数和最大公约数、C++ 实现求 N 个数的最大公约数和最小公倍数的相关知识，请在本站寻找。