如何捕获 UIViewAlertForUnsatisfiableConstraints？（如何捕获绿叶蜥）

25-02-24 15

本篇文章给大家谈谈如何捕获UIViewAlertForUnsatisfiableConstraints？，以及如何捕获绿叶蜥的知识点，同时本文还将给你拓展21、MVSNeRF:FastGenerali

本篇文章给大家谈谈如何捕获 UIViewAlertForUnsatisfiableConstraints？，以及如何捕获绿叶蜥的知识点，同时本文还将给你拓展21、MVSNeRF: Fast Generalizable Radiance Field Reconstruction from Multi-View Stereo、AI-Constraint Satisfaction Problems (CSP)、cocoa-touch – iOS5：有人设法用三个按钮和textfield(UIAlertViewStylePlainTextInput)修复UIAlertView吗？、Deformable ConvNets--Part2: Spatial Transfomer Networks(STN)等相关知识，希望对各位有所帮助，不要忘了收藏本站喔。

本文目录一览：

如何捕获 UIViewAlertForUnsatisfiableConstraints？（如何捕获绿叶蜥）
21、MVSNeRF: Fast Generalizable Radiance Field Reconstruction from Multi-View Stereo
AI-Constraint Satisfaction Problems (CSP)
cocoa-touch – iOS5：有人设法用三个按钮和textfield(UIAlertViewStylePlainTextInput)修复UIAlertView吗？
Deformable ConvNets--Part2: Spatial Transfomer Networks(STN)

如何捕获 UIViewAlertForUnsatisfiableConstraints？（如何捕获绿叶蜥）

我看到调试器日志中出现错误：

Will attempt to recover by breaking constraint 
<NSLayoutConstraint:0x191f0920 H:[MPKnockoutButton:0x17a876b0]-(34)-[MPDetailSlider:0x17a8bc50](LTR)>

Make a symbolic breakpoint at UIViewAlertForUnsatisfiableConstraints to catch this in the debugger.
The methods in the UIConstraintBasedLayoutDebugging category on UIView listed in <UIKit/UIView.h> may also be helpful.

我该如何打那个电话？它没有出现在我的代码中的任何地方。

截图1

21、MVSNeRF: Fast Generalizable Radiance Field Reconstruction from Multi-View Stereo

简介

主页：https://apchenstu.github.io/mvsnerf/

在这里插入图片描述

提出了一种新的神经渲染方法MVSNeRF，它可以有效地重建用于视图合成的神经辐射场。与先前关于神经辐射场的工作不同，这些工作考虑对密集捕获的图像进行逐场景优化，提出了一种通用的深度神经网络，该网络可以通过快速网络推理仅从三个附近的输入视图重建辐射场。利用plane-swept cost volumes(广泛用于multi-view stereo)进行几何感知场景推理，并将其与基于物理的体渲染相结合进行神经辐射场重建

Multi-view stereo

MVS是一个经典的计算机视觉问题，旨在使用从多个视点捕获的图像实现密集的几何结构重建dense geometry reconstruction

深度学习技术已被引入解决MVS问题。MVSNet 在参考视图的平面扫描成本体积上应用3D CNN进行深度估计，实现了优于经典传统方法的高质量3D重建

实现流程

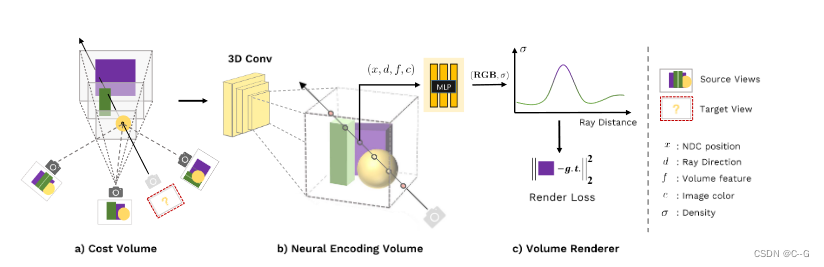
在这里插入图片描述

首先通过将二维图像特征扭曲到平面扫描上来构建一个cost volume(a)。然后，我们使用3D CNN来重建一个带有每个体素神经特征的neural encoding volume。我们使用MLP来回归任意位置的体积密度和RGB亮度，使用从encoding volume中插值的特征。这些体积特性被用于可微射线行进的最终渲染©。

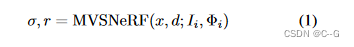
在这里插入图片描述

x代表3d位置，d是视图方向，σ是x方向的体密度，r是x处的输出亮度(RGB颜色)取决于观察方向d，捕获图像Ii，新视角相机参数Φi

Cost Volume

将m个输入图像中的2D图像特征扭曲到参考视图的挫折面上的一个平面扫描体，在参考视图reference view(i = 1)构建了一个cost volume P，允许几何感知场景理解

Extracting image features

使用深度二维CNN T来提取各个输入视图的二维图像特征，从而有效地提取代表局部图像外观的二维神经特征，使用下采样卷积层将图像Ii（H x W x 3）卷积为特征图Fi（H/4 x W/4 x C），C为通道数

在这里插入图片描述

Warping feature maps

通过给定的相机的内外参数Φ = [K, R, t]进行同形扭曲

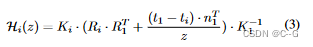
在这里插入图片描述

Hi（z）为视图i到深度z的参考视图的扭曲矩阵，K为本征矩阵，R和t是相机旋转矩阵和平移矩阵，所以特征图都进行如下变换

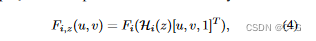
在这里插入图片描述

Fi,z 为深度z处的扭曲特征图，（u，v）为参考视图中的像素位置，在这里，使用参考视图中的归一化设备坐标 (NDC)来参数化(u，v，z)。

Cost volume

cost volumeP由D 扫描平面(sweeping planes)的扭曲特征图(warped feature maps)构造而成，利用基于方差的度量（variance-based metric）来计算成本（cost），对于以(u，v，z)为中心的P中的每个体素voxel，其成本特征向量cost feature vector由下式计算

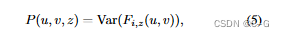
在这里插入图片描述

Var计算M个视图的方差，这种基于方差的成本体对不同输入视图上的图像外观变化进行编码；这解释了由场景几何体和视图相关的着色效果shading effects引起的外观变化

Radiance field reconstruction

利用3D CNN B从原始2D image feature costs的cost volume P中重建neural encoding volume S；S由编码局部场景几何形状和外观的每个体素特征组成。MLP decoder A 用于从该编码体回归体渲染属

Neural encoding volume

训练一个深度3D CNN B，将构建的image-feature cost volume转换为新的C通道神经特征体积 S，其中特征空间由网络自身学习和发现，用于后续的体积属性回归

在这里插入图片描述

3D CNN B是一个具有下采样和上采样卷积层和跳跃连接的3D UNet，可以有效地推断和传播场景外观信息，从而产生有意义的场景编码体S，网络可以学习在每个体素的神经特征中编码有意义的场景几何和外观；这些特征随后被连续地内插和改变

Regressing volume properties

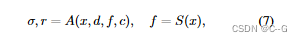
在这里插入图片描述

给定一个任意的3D位置x和一个观看方向d，我们使用MLP a从神经编码体积s回归相应的体积密度σ和视相关的亮度r

这里同时将原始图像Ii的像素颜色 c= [I(ui, vi)] （ (ui, vi)是在视图i上投影3D点x时的像素位置）作为额外输入，由于2D特征提取的下采样，场景编码体具有相对低的分辨率；仅从这些信息中回归高频出现是具有挑战性的。因此，引入了原始图像像素数据

f = S(x)是在位置x处从volume S三线性内插的神经特征

x在参考视图的NDC空间中被参数化，而d由参考视图坐标处的单位向量表示。使用NDC空间可以有效地归一化跨不同数据源的场景比例，有助于良好的可推广性

对位置和方向向量(x和d)应用了位置编码

补充细节

在得到体密度和视点相关辐射后，后续于原始NeRF基本一致.

整个框架模拟了一个神经辐射场，从几个(三个)输入图像回归场景中的体积密度和视点相关辐射率。此外，一旦场景编码体积S被重建，与MLP解码器A结合的该体积可以被独立使用，而无需预先考虑2D和3D CNNs。它们可以被视为辐射场的独立神经表示，输出体属性，从而支持体渲染。

效果

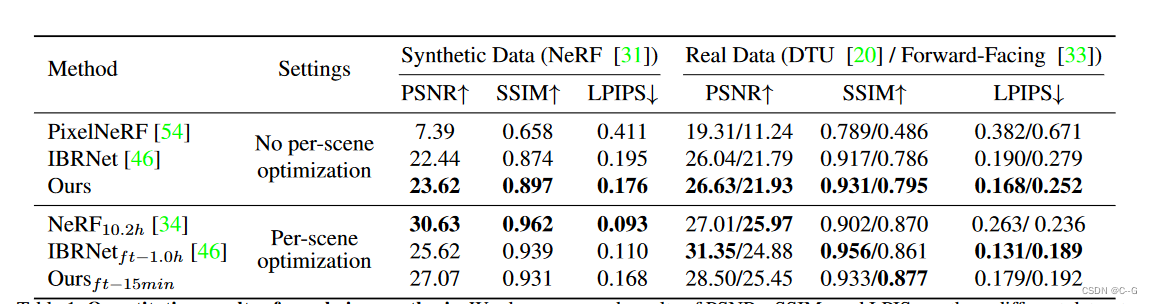
在这里插入图片描述

AI-Constraint Satisfaction Problems (CSP)

Constraint Satisfaction Problem

在搜索算法中，我们关心的是从初始节点到目标节点的一条路径；而在约束满足问题中，我们没有初始状态，只关心 goal 而不在乎 path。

Planning: sequences of actions
Identification: assignments to variables

Constraint Satisfaction Problems (CSPs) are specialized for identification problems

我们可以把 CSP 看成是特殊的搜索问题。对于一般的搜索问题来说，State is atomic or indivisible, known as a “black box” without internal structure，而在 CSP 中 State is represented as a feature vector；在搜索问题中 Goal test can be any function over states，而CSP 中 Goal test is a set of constraints to identify the allowable feature vector。

我们来仔细看看 Feature Vector，它是由 A set of k variables (or features) 组成的，对于每个 feature 有值域 domain；而我们的目标就是找到满足约束的一组赋值。方便起见我们定义 complete state 和 partial state，后者即对部分变量赋值满足约束，其余部分待赋值。典型的问题有 Map Coloring 和 N-Queens 等。

Constraint Graphs

对于一个 CSP 问题，我们可以采用约束图的方式进行表示：对于一个二元约束来说可将两个 feature 连起来；所以，问题在于将 N-nary 转化为 Binary constraints。我们假定 domain 都是有限的。

第一步，引入新的变量（约束）Z，例如对于加法的三元约束来说，我们引入变量，满足

Domain is the set of all possible 3-tuples satisfying $A+B=C$. ${(a_1 , b_1 , c 1 ), (a 2 , b 2 , c 2 ), …}， s.t. a_ 1 + b_ 1 = c_ 1 …$

第二步，建立新变量 Z 与 A、B、C 之间的约束，显然可以是 A 与 Z 的 domain 中三元组的第一个元素相同。

Create new constraints between Z and three original variables respectively (the position in the tuple is linked to an original variable).

$$ (Z,A)\in {((a_1,b_1,c_1)a_1),...}\tag{1}\ (Z,B)\in {((a_1,b_1,c_1)b_1),...} $$

这样，我们通过引入一个新的变量，和三个二元约束，就把该三元约束转换好了；对于更多的约束，可以用相似的方法进行。

Note：这里可能一时没法理解，我们要理解究竟什么是约束。先来看普通的二元约束，以地图问题为例，假设每个国家的颜色均可为红黄蓝，约束的意义在于，若 A 填了红色，那么相邻的 B 就只能涂黄或蓝——也就是说，一个变量的值确定后，另一个变量的值域也变化了——反过来想我们如何表示约束？可以采用集合的形式 ${(R,Y),(R,B)...}$ 。我们重新来理解约束，就是 A 和 B 分别取值，构成一个二元组，要求这个二元组在约束集合中。（我在理解上的困惑实际上在于，没有搞清楚约束的形式化表达。）这样的话，我们来看加法约束，假设 A 已定，对于 A 和 Z 的约束来说，式（1）要求两者构成的二元组要在约束集合中，这样就缩减了 Z 的值域；若进一步定下了 B 的值，Z 的值域将进一步缩小，事实上这时仅可能剩下一个三元组 $(a,b,c=a+b)$ ，接下来可对 C 进行赋值或者检测约束是否满足。

Solving CSPs

我们可采用 Standard search formulation of CSPs，我们的初始状态为一个 empty assignment，后继函数为对任一未赋值变量进行赋值，而目标检测则要求赋值为 complete state 且符合约束。显然，1. 我们只检查了叶节点而事实上在过程中就可以进行约束检查；2. 如前所述，我们并不关心赋值的顺序，只关心 goal。注意到无论是 BFS 还是 DFS 都是低效的，但是我们没必要存储中间节点，因此，要在 DFS 框架下进行改进。

Backtracking Search 算法针对了这两个问题进行了改进

Idea 1: One variable at a time in fixed ordering
Idea 2: Check constraints as you go

简言之：Backtracking = DFS + variable-ordering + fail-on-violation

两个思路都是比较直观的不多介绍。

现在的问题在于，如何 Improving Backtracking。

Ordering

显见，不同的赋值顺序会对效率产生影响，又可分为两类：Which variable should be assigned next? In what order should its values be tried?

对于变量的顺序来说，直观来讲，为了尽早避免可能的冲突，我们会选取那些约束比较多的变量（或者说，是 domain 比较小的，回忆一下约束的意义即在于，某一变量定值之后会缩减另外的变量的 domain）。例如，在地图着色问题中，我们一般会从已着色的国家的相邻国开始进行着色。定义：

Variable Ordering: Minimum remaining values (MRV)

Choose the variable with the fewest legal left values in its domain. Also called “most constrained variable”

“Fail-fast” ordering

对于赋值的顺序来说，我们要尽早找到一组解（而不是回溯），那么我们肯定希望给剩余的变量更多的「可能性」，也就是说要避免其他变量的取值发生缩减；我们定义

Value Ordering: Least Constraining Value (LSV)

Given a choice of variable, choose the least constraining value. I.e., the one that rules out the fewest values in the remaining variables

Note that it may take some computation to determine this! (E.g., rerunning filtering)

注意，前者可以让我们避免一些可能的错误（可以**「剪枝」**）；而或者只是提高了找到解的可能性（但并非保障，只能说「更快找到」）。若我们想找到全部的解，那么前者可以帮助减少计算，但后者则并不会有什么助益。

Filtering: Can we detect inevitable failure early?

MRV 可以让我们避免一些简单的错误（如相邻两国填同样的颜色），然而这里我们仅仅检测了这样一个简单的约束；那么我们能否采取更多的计算来提前发现错误呢？这就是 Filtering 的思路。

我们先来看Forward Checking：Cross off values that violate a constraint when added to the existing assignment。我们在取定一个值（搜索）之后，对于相邻边的 domain 进行缩减（推理）。当然，这里我们只「向前看」了一步，事实上对于缩减了 domain 的变量我们可以继续进行推理，也就是约束传播 Constraint Propagation 。我们来给出定义：

Consistency of A Single Arc

An arc $X \rightarrow Y$ is consistent iff for every $x$ in the tail there is some $y$ in the head which could be assigned without violating a constraint

Forward checking: Enforcing consistency of arcs pointing to each new assignment

注意定义，对于一条弧 $X \rightarrow Y$ 来说，我们给定Y/减小了其值域之后，要进行缩减的是 X 的值域；如何缩减，就是要使得 X 的任一个取值，Y 中都至少有一个能满足约束——对于那么不满足的 X 的取值，我们进行缩减。注意其方向，按照这个定义，我们在做 Forward checking 的时候，给定了 A，那么就要对于所以包含指向 A 的弧（事实上都是无向边）的变量进行值域缩减。下面给出具体的算法：

更宏观的解释：在 Filtering 中，我们交替进行搜索和推理，在为某一变量赋值之后做弧相容检查。具体来说，当$X_i$赋值后，我们调用$AC-3$，从$(X_j,X_i)$中未赋值变量$X_j$开始，进行约束传播；事实上我们维护了一个队列，一旦某一个变量的值域发生了变化，就将其 neighbors 加入其中。

然而，弧相容仍不能保证不进行回溯。例如，对于一个三角形来说，若每个节点只能赋值为红蓝两色那么显然是无解的，但用弧相容找不错错误来。若想直接得到解，我么引入k-相容 K-Consistency 的概念：

1-Consistency (Node Consistency): Each single node’s domain has a value which meets that node’s unary constraints
2-Consistency (Arc Consistency): For each pair of nodes, any consistent assignment to one can be extended to the other
K-Consistency: For each k nodes, any consistent assignment to k-1 can be extended to the k th node.

并给出强 k-相容 Strong k-consistency: also k-1, k-2, … 1 consistent，以及结论，对于一个 n 变量的 CSP 来说，strong n-consistency means we can solve without backtracking。这是显然的。

Structure: Can we exploit the problem structure?

这里问题的结果指的是约束图的结构。考虑极端情况：所有节点结构独立的，那么我们可以任意赋值；更为一般的，Independent sub-problems are identifiable as connected components of constraint graph。事实上，这样可分割的情况是很少见的（如澳大利亚地图着色），一个理想的可分问题能大大降低复杂度。注意到，我们可以用 Search 问题的通用复杂度来衡量 CSP，搜索树的深度显然是节点数，宽度为 domain 的大小；若一个 n 个节点的问题可分割成大小为 c 的若干子问题，则时间复杂度从 $O(d^n)$ 降为 $O({n \over c} d^c)$ ，变成了 n 的线性函数。

可分割为 sub-problems 的问题也是很少见的，一个更一般的情况是 Tree-Structured CSPs，对此我们有定理：

Theorem: if the constraint graph has no loops, the CSP can be solved in $O(n d^2 )$ time

同样变为了 n 的线性函数。如何做到呢？1. 对约束树进行拓扑排序；2. 逆着拓扑排序，从孩子到父节点做弧相容检查（即对于$(Parent(X_j),X_j)$进行检查）；3. 然后顺着拓扑排序，从根节点到到叶节点进行赋值。注意到，进行这样一次弧相容检查之后，我们保障了对于父节点的任意取值，子节点都至少有一个值满足约束，也就保障了算法的正确性（解的存在性）。

树结构也太少见了，一个拓展是 Nearly Tree-Structured CSPs 。对其的思路是，选定一组变量，使得删去这些之后的节点构成一棵树，这样的话，我们只要遍历这组节点的所有可能赋值情况即可。

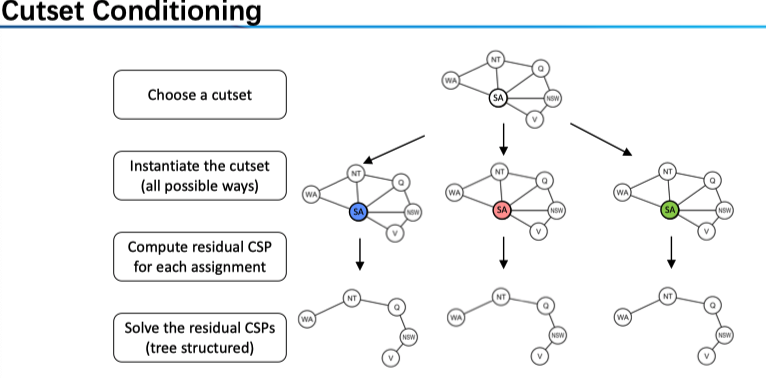
Conditioning: instantiate a variable, prune its neighbors'' domains

Cycle Cutset conditioning: instantiate (in all ways) a set of variables such that the remaining constraint graph is a tree.

所以我们的任务是找到这样的 Cycle Cutset，若其大小为 c，则找到这个集合之后，搜索的时间复杂度为 $O( (d^c ) (n-c) d^2)$

Iterative Improvement

在上述 Backtracking 算法中，我们仍一个一个对变量进行赋值，但 CSP 只关心结果，因此一个自然的想法是直接从 complete state 出发，寻找解。Iterative Improvement 是一种 Local Search 方法。我们

Take an assignment with unsatisfied constraints
然后 Operators reassign variable values。

具体来说，我们 1. Variable selection: randomly select any conflicted variable；2. Value selection: min-conflicts heuristic: Choose a value that violates the fewest constraints。这里第二步的变量选择使得冲突最少的那一个，可以认为是一种 heuristic $h(n)=$ #total number of violated constraints。

这里体现的是 Local Search versus Systematic Search，相较于 BFS, DFS, IDS, Best-First, A* 等系统搜索算法（Keeps some history of visited nodes）来说，后者的一大特点就是不保留 history，然而，这在减少了存储负担的情况带来的问题则是失去了 complet 性质，容易陷入局部最优。

一些 Local Search 包括

Hill climbing：在 neighbor 中找最优值，迭代，可能陷入局部最优
Simulated annealing：结合了 random walk 和 hill climbing。在循环过程汇总，与 hill climbing 的不同在于，对于 next state 来说，若是较为「好的」则以概率 1 接受；若相较于前一个状态变差了不是直接拒绝而是以一定的概率 $P(T)$ 接受（random walk）。接受的概率随着时间降低，也就是「模拟退火」的命名原因。具体的，接受概率为 T 的函数，如 $\exp(\Delta E/T)$ 其中 $\Delta E$ 可表为 next value - current value，而$T$ 随着时间而降低，即从 random walk 逐渐变为 hill climbing。
Local beam search：并行 k 个 hill climbing——对于 Systematic search 来说保留所有的历史，而前两种仅保留一个，都太极端了，Local beam search 每次保留 k 个 complete state 而它们的 successor 中找最好的（加入了 randomness）的 k 个后代进行下一次模拟。
Genetic algorithm

另，对于连续函数来说，则要采用梯度下降方法 Gradient decent。

进一步阅读：《人工智能》chapter 4.1 – 4.2。

cocoa-touch – iOS5：有人设法用三个按钮和textfield(UIAlertViewStylePlainTextInput)修复UIAlertView吗？

苹果真的搞砸了这个.我想使用带有新UIAlertViewStylePlainTextInput样式的UIAlertView并在其中有三个按钮.结果如下：

有人设法建立一个解决方法,直到Apple解决了这个问题吗？也许以某种方式降低按钮高度或增加警报视图的总高度？

解决方法

这不是一个完整的解决方案,但它可能会让你开始.

UIAlertView view = new UIAlertView ("Alert","This is an alert\n\n\n",null,"Login","One","Two");

UIView theTextField = new UIView (new RectangleF (12.0f,80.0f,260.0f,25.0f));
UITextView txt = new UITextView (new RectangleF (0f,0f,25.0f));
txt.BackgroundColor = UIColor.White;
theTextField.AddSubview (txt);
view.AddSubview (theTextField); 

view.Show ();

我发现当您将文本视图添加为子视图时,AlertView会尝试智能化.但是如果你把一个通用的UIView放在一个容器中,它会给你一些更有用的东西.

我还验证了这是XCode中的一个问题.

这post可能会给你一些更多的想法.

Deformable ConvNets--Part2: Spatial Transfomer Networks(STN)

转自：https://blog.csdn.net/u011974639/article/details/79681455

<div id="content_views">  <svg xmlns="http://www.w3.org/2000/svg"><path stroke-linecap="round" d="M5,0 0,2.5 5,5z" id="raphael-marker-block"></path></svg> <h1 id="deformable-convnet 简介"><a name="t0"></a>Deformable ConvNet 简介 </h1>

关于 Deformable Convolutional Networks 的论文解读，共分为 5 个部分，本章是第二部分：

<ul> <li>[ ] Part1：快速学习实现仿射变换 </li> <li>[x] Part2： Spatial Transfomer Networks 论文解读 </li> <li>[ ] Part3： TenosorFlow 实现 STN</li> <li>[ ] Part4： Deformable Convolutional Networks 论文解读 </li> <li>[ ] Part5： TensorFlow 实现 Deformable ConvNets</li> </ul>

本章解读 Spatial Transfomer Networks 论文，看 STN 是如何将仿射变换加入到现有 CNN 架构上，并使之支持端对端训练。

<h1 id="spatial-transformer-networks"><a name="t1"></a>Spatial Transformer Networks</h1>

STN:Spatial Transformer Networks

收录：NIPS 2015 (Advances in Neural Information Processing Systems 28)

原文地址：<a href="http://papers.nips.cc/paper/5854-spatial-transformer-networks.pdf" rel="nofollow" target="_blank">STN</a>

代码:

<ul> <li><a href="https://github.com/qassemoquab/stnbhwd" rel="nofollow" target="_blank">torch</a></li> <li><a href="https://github.com/daviddao/spatial-transformer-tensorflow" rel="nofollow" target="_blank">TensorFlow</a></li> </ul>

<hr>

<h1 id="motivation"><a name="t2"></a>Motivation</h1>

在实际场景，不同的场景下目标会存在不同状态，如下图：

对于相同目标物，不一样的尺度缩放、形变、背景干扰、观察视角，获取到的目标信息都是不同的，这极大的增加了目标检测等任务的难度。

针对这一问题，大多数先进系统的解决办法是，对模型的训练数据做数据增强，例如随机的 crop (裁剪)、平移、放缩、旋转等操作，通过增加数据量，进而增加模型的泛化能力。

<h2 id="池化存在的问题"><a name="t4"></a > 池化存在的问题 </h2>

先引 Hinton 对池化操作的评价：

The pooling operation used in convolutional neural networks is a big mistake and the fact that it works so well is a disaster. (Geoffrey Hinton, Reddit AMA)

池化层在接收复杂输入的基础上，将复杂输入分成若干 cell，提取成简单的 cell，目标简单的旋转或平移，经过几层的池化提取的信息就比较相似了，通过不断简化输入聚合像素值，模型内部重复的池化操作，可让模型对目标有 内在不变性 ：

关于池化层存在的问题，在前面的 blog 里面已经讲了很多遍。池化操作是破坏性的，丢弃了 75% 的输入信息，虽然模型增加了健壮性但也丢弃了细节信息。

除了这一问题，池化层受限于自身架构上的限制，只能获取 局部信息和固定的变换结构 ，这只有很小的感受野，通过不断加深网络层次，获得更大的感受野。我们不能随意的调整池化层的大小，因为这会急剧的降低特征映射的空间分辨率。

<hr>

<h1 id="spatial-transformer-networks-1"><a name="t5"></a>Spatial Transformer Networks</h1>

针对上面提到的问题，DeepMind 的 < a href="https://arxiv.org/pdf/1506.02025.pdf" rel="nofollow" target="_blank">STN:Spatial Transformer Networks</a > 工作开创性的在 CNN 中引入通过加入空间变换层达到仿射变换目的。STN 模型优点在于：

<ul> <li> 模块化 ：STN 可以很方便的集成到现存的 CNN 架构中 </li> <li> 可微分 ：STN 可通过 BP 优化参数，支持 end-2-end 训练 </li> <li> 动态性 ：STN 相比于池化等操作，可动态的将仿射变换应用于采样点上 </li> </ul>

仿射变换示意图：

<ul> <li > 图 (a) 是常规的恒等变换，在输入 <spanid="MathJax-Element-75-Frame" tabindex="0"data-mathml="<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>U</mi></math>" role="presentation"><spanid="MathJax-Span-1"><spanid="MathJax-Span-2"><spanid="MathJax-Span-3">U<spanrole="presentation"><math xmlns="http://www.w3.org/1998/Math/MathML"><mi>U</mi></math><script type="math/tex" id="MathJax-Element-75">U</script > 上采样网格，得到输出 <spanid="MathJax-Element-76-Frame" tabindex="0"data-mathml="<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>V</mi></math>" role="presentation"><spanid="MathJax-Span-4"><spanid="MathJax-Span-5"><spanid="MathJax-Span-6">V<spanrole="presentation"><math xmlns="http://www.w3.org/1998/Math/MathML"><mi>V</mi></math><script type="math/tex" id="MathJax-Element-76">V</script></li> <li > 图 (b) 是采样是做了仿射变换，输入 <spanid="MathJax-Element-77-Frame" tabindex="0"data-mathml="<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>U</mi></math>" role="presentation"><spanid="MathJax-Span-7"><spanid="MathJax-Span-8"><spanid="MathJax-Span-9">U<spanrole="presentation"><math xmlns="http://www.w3.org/1998/Math/MathML"><mi>U</mi></math><script type="math/tex" id="MathJax-Element-77">U</script > 上采样使用的仿射变换后的网格，最终得到 <spanid="MathJax-Element-78-Frame" tabindex="0"data-mathml="<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>U</mi></math>" role="presentation"><spanid="MathJax-Span-10"><spanid="MathJax-Span-11"><spanid="MathJax-Span-12">U<spanrole="presentation"><math xmlns="http://www.w3.org/1998/Math/MathML"><mi>U</mi></math><script type="math/tex" id="MathJax-Element-78">U</script></li> </ul>

由 Part1 可知，当 <spanid="MathJax-Element-79-Frame" tabindex="0"data-mathml="<math xmlns="http://www.w3.org/1998/Math/MathML"><msub><mi>T</mi><mrow class="MJX-TeXAtom-ORD"><mi>&#x03B8;</mi></mrow></msub></math>" role="presentation"><spanid="MathJax-Span-13"><spanid="MathJax-Span-14"><spanid="MathJax-Span-15"><spanid="MathJax-Span-16">T<spanid="MathJax-Span-17"><spanid="MathJax-Span-18"><spanid="MathJax-Span-19">θ<spanrole="presentation"><math xmlns="http://www.w3.org/1998/Math/MathML"><msub><mi>T</mi><mrow><mi>θ</mi></mrow></msub></math><script type="math/tex" id="MathJax-Element-79">T_{\theta}</script > 是 2D 方式变换，坐标变换为： <div></div><div><spanid="MathJax-Element-80-Frame" tabindex="0"data-mathml="<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"><mrow><mo>(</mo><mtable rowspacing="4pt" columnspacing="1em"><mtr><mtd><msubsup><mi>x</mi><mi>i</mi><mi>s</mi></msubsup></mtd></mtr><mtr><mtd><msubsup><mi>y</mi><mi>i</mi><mi>s</mi></msubsup></mtd></mtr></mtable><mo>)</mo></mrow><mo>=</mo><msub><mi>T</mi><mrow class="MJX-TeXAtom-ORD"><mi>&#x03B8;</mi></mrow></msub><mo stretchy="false">(</mo><msub><mi>G</mi><mi>i</mi></msub><mo stretchy="false">)</mo><mo>=</mo><msub><mi>A</mi><mrow class="MJX-TeXAtom-ORD"><mi>&#x03B8;</mi></mrow></msub><mrow><mo>(</mo><mtable rowspacing="4pt" columnspacing="1em"><mtr><mtd><msubsup><mi>x</mi><mi>i</mi><mi>t</mi></msubsup></mtd></mtr><mtr><mtd><msubsup><mi>y</mi><mi>i</mi><mi>t</mi></msubsup></mtd></mtr><mtr><mtd><mn>1</mn></mtd></mtr></mtable><mo>)</mo></mrow><mo>=</mo><mrow><mo>[</mo><mtable rowspacing="4pt" columnspacing="1em"><mtr><mtd><msub><mi>&#x03B8;</mi><mrow class="MJX-TeXAtom-ORD"><mn>11</mn></mrow></msub></mtd><mtd><msub><mi>&#x03B8;</mi><mrow class="MJX-TeXAtom-ORD"><mn>12</mn></mrow></msub></mtd><mtd><msub><mi>&#x03B8;</mi><mrow class="MJX-TeXAtom-ORD"><mn>13</mn></mrow></msub></mtd></mtr><mtr><mtd><msub><mi>&#x03B8;</mi><mrow class="MJX-TeXAtom-ORD"><mn>21</mn></mrow></msub></mtd><mtd><msub><mi>&#x03B8;</mi><mrow class="MJX-TeXAtom-ORD"><mn>22</mn></mrow></msub></mtd><mtd><msub><mi>&#x03B8;</mi><mrow class="MJX-TeXAtom-ORD"><mn>23</mn></mrow></msub></mtd></mtr></mtable><mo>]</mo></mrow><mrow><mo>(</mo><mtable rowspacing="4pt" columnspacing="1em"><mtr><mtd><msubsup><mi>x</mi><mi>i</mi><mi>t</mi></msubsup></mtd></mtr><mtr><mtd><msubsup><mi>y</mi><mi>i</mi><mi>t</mi></msubsup></mtd></mtr><mtr><mtd><mn>1</mn></mtd></mtr></mtable><mo>)</mo></mrow></math>" role="presentation"><spanid="MathJax-Span-20"><spanid="MathJax-Span-21"><spanid="MathJax-Span-22"><spanid="MathJax-Span-23">(<spanid="MathJax-Span-24"><spanid="MathJax-Span-25"><spanid="MathJax-Span-26"><spanid="MathJax-Span-27"><spanid="MathJax-Span-28">x<spanid="MathJax-Span-29">s<spanid="MathJax-Span-30">i<spanid="MathJax-Span-31"><spanid="MathJax-Span-32"><spanid="MathJax-Span-33"><spanid="MathJax-Span-34">y<spanid="MathJax-Span-35">s<spanid="MathJax-Span-36">i<spanid="MathJax-Span-37">)<spanid="MathJax-Span-38">=<spanid="MathJax-Span-39"><spanid="MathJax-Span-40">T<spanid="MathJax-Span-41"><spanid="MathJax-Span-42"><spanid="MathJax-Span-43">θ<spanid="MathJax-Span-44">(<spanid="MathJax-Span-45"><spanid="MathJax-Span-46">G<spanid="MathJax-Span-47">i<spanid="MathJax-Span-48">)<spanid="MathJax-Span-49">=<spanid="MathJax-Span-50"><spanid="MathJax-Span-51">A<spanid="MathJax-Span-52"><spanid="MathJax-Span-53"><spanid="MathJax-Span-54">θ<spanid="MathJax-Span-55"><spanid="MathJax-Span-56">⎛⎝⎜⎜⎜<spanid="MathJax-Span-57"><spanid="MathJax-Span-58"><spanid="MathJax-Span-59"><spanid="MathJax-Span-60"><spanid="MathJax-Span-61">x<spanid="MathJax-Span-62">t<spanid="MathJax-Span-63">i<spanid="MathJax-Span-64"><spanid="MathJax-Span-65"><spanid="MathJax-Span-66"><spanid="MathJax-Span-67">y<spanid="MathJax-Span-68">t<spanid="MathJax-Span-69">i<spanid="MathJax-Span-70"><spanid="MathJax-Span-71"><spanid="MathJax-Span-72">1<spanid="MathJax-Span-73">⎞⎠⎟⎟⎟<spanid="MathJax-Span-74">=<spanid="MathJax-Span-75"><spanid="MathJax-Span-76">[<spanid="MathJax-Span-77"><spanid="MathJax-Span-78"><spanid="MathJax-Span-79"><spanid="MathJax-Span-80"><spanid="MathJax-Span-81">θ<spanid="MathJax-Span-82"><spanid="MathJax-Span-83"><spanid="MathJax-Span-84">11<spanid="MathJax-Span-99"><spanid="MathJax-Span-100"><spanid="MathJax-Span-101"><spanid="MathJax-Span-102">θ<spanid="MathJax-Span-103"><spanid="MathJax-Span-104"><spanid="MathJax-Span-105">21<spanid="MathJax-Span-85"><spanid="MathJax-Span-86"><spanid="MathJax-Span-87"><spanid="MathJax-Span-88">θ<spanid="MathJax-Span-89"><spanid="MathJax-Span-90"><spanid="MathJax-Span-91">12<spanid="MathJax-Span-106"><spanid="MathJax-Span-107"><spanid="MathJax-Span-108"><spanid="MathJax-Span-109">θ<spanid="MathJax-Span-110"><spanid="MathJax-Span-111"><spanid="MathJax-Span-112">22<spanid="MathJax-Span-92"><spanid="MathJax-Span-93"><spanid="MathJax-Span-94"><spanid="MathJax-Span-95">θ<spanid="MathJax-Span-96"><spanid="MathJax-Span-97"><spanid="MathJax-Span-98">13<spanid="MathJax-Span-113"><spanid="MathJax-Span-114"><spanid="MathJax-Span-115"><spanid="MathJax-Span-116">θ<spanid="MathJax-Span-117"><spanid="MathJax-Span-118"><spanid="MathJax-Span-119">23<spanid="MathJax-Span-120">]<spanid="MathJax-Span-121"><spanid="MathJax-Span-122">⎛⎝⎜⎜⎜<spanid="MathJax-Span-123"><spanid="MathJax-Span-124"><spanid="MathJax-Span-125"><spanid="MathJax-Span-126"><spanid="MathJax-Span-127">x<spanid="MathJax-Span-128">t<spanid="MathJax-Span-129">i<spanid="MathJax-Span-130"><spanid="MathJax-Span-131"><spanid="MathJax-Span-132"><spanid="MathJax-Span-133">y<spanid="MathJax-Span-134">t<spanid="MathJax-Span-135">i<spanid="MathJax-Span-136"><spanid="MathJax-Span-137"><spanid="MathJax-Span-138">1<spanid="MathJax-Span-139">⎞⎠⎟⎟⎟<spanrole="presentation"><math xmlns="http://www.w3.org/1998/Math/MathML" display="block"><mrow><mo>(</mo><mtable rowspacing="4pt" columnspacing="1em"><mtr><mtd><msubsup><mi>x</mi><mi>i</mi><mi>s</mi></msubsup></mtd></mtr><mtr><mtd><msubsup><mi>y</mi><mi>i</mi><mi>s</mi></msubsup></mtd></mtr></mtable><mo>)</mo></mrow><mo>=</mo><msub><mi>T</mi><mrow><mi>θ</mi></mrow></msub><mo stretchy="false">(</mo><msub><mi>G</mi><mi>i</mi></msub><mo stretchy="false">)</mo><mo>=</mo><msub><mi>A</mi><mrow><mi>θ</mi></mrow></msub><mrow><mo>(</mo><mtable rowspacing="4pt" columnspacing="1em"><mtr><mtd><msubsup><mi>x</mi><mi>i</mi><mi>t</mi></msubsup></mtd></mtr><mtr><mtd><msubsup><mi>y</mi><mi>i</mi><mi>t</mi></msubsup></mtd></mtr><mtr><mtd><mn>1</mn></mtd></mtr></mtable><mo>)</mo></mrow><mo>=</mo><mrow><mo>[</mo><mtable rowspacing="4pt" columnspacing="1em"><mtr><mtd><msub><mi>θ</mi><mrow><mn>11</mn></mrow></msub></mtd><mtd><msub><mi>θ</mi><mrow><mn>12</mn></mrow></msub></mtd><mtd><msub><mi>θ</mi><mrow><mn>13</mn></mrow></msub></mtd></mtr><mtr><mtd><msub><mi>θ</mi><mrow><mn>21</mn></mrow></msub></mtd><mtd><msub><mi>θ</mi><mrow><mn>22</mn></mrow></msub></mtd><mtd><msub><mi>θ</mi><mrow><mn>23</mn></mrow></msub></mtd></mtr></mtable><mo>]</mo></mrow><mrow><mo>(</mo><mtable rowspacing="4pt" columnspacing="1em"><mtr><mtd><msubsup><mi>x</mi><mi>i</mi><mi>t</mi></msubsup></mtd></mtr><mtr><mtd><msubsup><mi>y</mi><mi>i</mi><mi>t</mi></msubsup></mtd></mtr><mtr><mtd><mn>1</mn></mtd></mtr></mtable><mo>)</mo></mrow></math></div><script type="math/tex; mode=display" id="MathJax-Element-80">\begin {pmatrix} x_i^s\\ y_i^s \end {pmatrix}=T_{\theta}(G_i) = A_{\theta}\begin {pmatrix} x_i^t\\ y_i^t \\ 1 \end {pmatrix} =\begin {bmatrix} \theta_{11}&\theta_{12} &\theta_{13} \\ \theta_{21}&\theta_{22} & \theta_{23} \end {bmatrix} \begin {pmatrix} x_i^t\\ y_i^t \\1 \end {pmatrix}</script>

<spanid="MathJax-Element-81-Frame" tabindex="0"data-mathml="<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">(</mo><msubsup><mi>x</mi><mi>i</mi><mi>s</mi></msubsup><mo>,</mo><msubsup><mi>y</mi><mi>i</mi><mi>s</mi></msubsup><mo stretchy="false">)</mo></math>" role="presentation"><spanid="MathJax-Span-140"><spanid="MathJax-Span-141"><spanid="MathJax-Span-142">(<spanid="MathJax-Span-143"><spanid="MathJax-Span-144">x<spanid="MathJax-Span-145">s<spanid="MathJax-Span-146">i<spanid="MathJax-Span-147">,<spanid="MathJax-Span-148"><spanid="MathJax-Span-149">y<spanid="MathJax-Span-150">s<spanid="MathJax-Span-151">i<spanid="MathJax-Span-152">)<spanrole="presentation"><math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">(</mo><msubsup><mi>x</mi><mi>i</mi><mi>s</mi></msubsup><mo>,</mo><msubsup><mi>y</mi><mi>i</mi><mi>s</mi></msubsup><mo stretchy="false">)</mo></math><script type="math/tex" id="MathJax-Element-81">(x_i^s,y_i^s)</script > 是源特征映射 (Source) 中采样点，<spanid="MathJax-Element-82-Frame" tabindex="0"data-mathml="<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">(</mo><msubsup><mi>x</mi><mi>i</mi><mi>t</mi></msubsup><mo>,</mo><msubsup><mi>y</mi><mi>i</mi><mi>t</mi></msubsup><mo stretchy="false">)</mo></math>" role="presentation"><spanid="MathJax-Span-153"><spanid="MathJax-Span-154"><spanid="MathJax-Span-155">(<spanid="MathJax-Span-156"><spanid="MathJax-Span-157">x<spanid="MathJax-Span-158">t<spanid="MathJax-Span-159">i<spanid="MathJax-Span-160">,<spanid="MathJax-Span-161"><spanid="MathJax-Span-162">y<spanid="MathJax-Span-163">t<spanid="MathJax-Span-164">i<spanid="MathJax-Span-165">)<spanrole="presentation"><math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">(</mo><msubsup><mi>x</mi><mi>i</mi><mi>t</mi></msubsup><mo>,</mo><msubsup><mi>y</mi><mi>i</mi><mi>t</mi></msubsup><mo stretchy="false">)</mo></math><script type="math/tex" id="MathJax-Element-82">(x_i^t,y_i^t)</script > 是仿射变换目标输出。<spanid="MathJax-Element-83-Frame" tabindex="0"data-mathml="<math xmlns="http://www.w3.org/1998/Math/MathML"><msub><mi>A</mi><mrow class="MJX-TeXAtom-ORD"><mi>&#x03B8;</mi></mrow></msub></math>" role="presentation"><spanid="MathJax-Span-166"><spanid="MathJax-Span-167"><spanid="MathJax-Span-168"><spanid="MathJax-Span-169">A<spanid="MathJax-Span-170"><spanid="MathJax-Span-171"><spanid="MathJax-Span-172">θ<spanrole="presentation"><math xmlns="http://www.w3.org/1998/Math/MathML"><msub><mi>A</mi><mrow><mi>θ</mi></mrow></msub></math><script type="math/tex" id="MathJax-Element-83">A_{\theta}</script > 是仿射变换矩阵。注意到上式是从目标通过变换矩阵就计算出源输入。

<h1 id="仿射变换层"><a name="t6"></a > 仿射变换层 </h1>

STN 中核心的 < code>Spatial Transformer</code > 变换如下：

整个 Spatial Transformer 分为以下几个部分：

<ul> <li><code>Localisation net</code>，用于获取仿射矩阵，即各个 <spanid="MathJax-Element-84-Frame" tabindex="0"data-mathml="<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>&#x03B8;</mi></math>" role="presentation"><spanid="MathJax-Span-173"><spanid="MathJax-Span-174"><spanid="MathJax-Span-175">θ<spanrole="presentation"><math xmlns="http://www.w3.org/1998/Math/MathML"><mi>θ</mi></math><script type="math/tex" id="MathJax-Element-84">\theta</script > 值。</li> <li><code>Grid generator</code>，用于生成采样坐标 </li> <li><code>Sampler</code>，实际对 <spanid="MathJax-Element-85-Frame" tabindex="0"data-mathml="<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>U</mi></math>" role="presentation"><spanid="MathJax-Span-176"><spanid="MathJax-Span-177"><spanid="MathJax-Span-178">U<spanrole="presentation"><math xmlns="http://www.w3.org/1998/Math/MathML"><mi>U</mi></math><script type="math/tex" id="MathJax-Element-85">U</script > 的采样 </li> </ul>

注意一下： 在 Part1 中，讲解使用双线性插值实现仿射变换，这是仿射变换层的核心基础。

<h2 id="localisation-net"><a name="t7"></a>Localisation net</h2>

<code>localisation network</code > 的目标是在输入特征映射上应用卷积或 FC 层，获取到仿射变换矩阵参数 <spanid="MathJax-Element-86-Frame" tabindex="0"data-mathml="<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>&#x03B8;</mi></math>" role="presentation"><spanid="MathJax-Span-179"><spanid="MathJax-Span-180"><spanid="MathJax-Span-181">θ<spanrole="presentation"><math xmlns="http://www.w3.org/1998/Math/MathML"><mi>θ</mi></math><script type="math/tex" id="MathJax-Element-86">\theta</script>，结构如下：

<ul> <li>input: 特征映射 <spanid="MathJax-Element-87-Frame" tabindex="0"data-mathml="<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>U</mi></math>" role="presentation"><spanid="MathJax-Span-182"><spanid="MathJax-Span-183"><spanid="MathJax-Span-184">U<spanrole="presentation"><math xmlns="http://www.w3.org/1998/Math/MathML"><mi>U</mi></math><script type="math/tex" id="MathJax-Element-87">U</script>，shape 为 <spanid="MathJax-Element-88-Frame" tabindex="0"data-mathml="<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">(</mo><mi>H</mi><mo>,</mo><mi>W</mi><mo>,</mo><mi>C</mi><mo stretchy="false">)</mo></math>" role="presentation"><spanid="MathJax-Span-185"><spanid="MathJax-Span-186"><spanid="MathJax-Span-187">(<spanid="MathJax-Span-188">H<spanid="MathJax-Span-189">,<spanid="MathJax-Span-190">W<spanid="MathJax-Span-191">,<spanid="MathJax-Span-192">C<spanid="MathJax-Span-193">)<spanrole="presentation"><math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">(</mo><mi>H</mi><mo>,</mo><mi>W</mi><mo>,</mo><mi>C</mi><mo stretchy="false">)</mo></math><script type="math/tex" id="MathJax-Element-88">(H,W,C)</script></li> <li>output: 仿射矩阵参数 <spanid="MathJax-Element-89-Frame" tabindex="0"data-mathml="<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>&#x03B8;</mi></math>" role="presentation"><spanid="MathJax-Span-194"><spanid="MathJax-Span-195"><spanid="MathJax-Span-196">θ<spanrole="presentation"><math xmlns="http://www.w3.org/1998/Math/MathML"><mi>θ</mi></math><script type="math/tex" id="MathJax-Element-89">\theta</script>，shape 为 <spanid="MathJax-Element-90-Frame" tabindex="0"data-mathml="<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">(</mo><mn>6</mn><mo>,</mo><mo stretchy="false">)</mo></math>" role="presentation"><spanid="MathJax-Span-197"><spanid="MathJax-Span-198"><spanid="MathJax-Span-199">(<spanid="MathJax-Span-200">6<spanid="MathJax-Span-201">,<spanid="MathJax-Span-202">)<spanrole="presentation"><math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">(</mo><mn>6</mn><mo>,</mo><mo stretchy="false">)</mo></math><script type="math/tex" id="MathJax-Element-90">(6,)</script></li> <li>architecture: 全连接层或卷积层 </li> </ul>

<code>Localisation net</code > 在实际训练过程中不断学习变换的参数。

<h2 id="grid-generator"><a name="t8"></a>Grid generator</h2>

<code>Grid generator</code > 干的事就是输出采样网格，即在输入中采样的点生成期望的转换输出。

普通的变换：

输入和输出的采样点是相同的。

仿射变换：

我们想通过目标采样网格经过仿射变换获取到实际在输入上采样网格点。

具体来讲，<code>Grid generator</code > 和 Part1 中讲的使用双线性插值实现仿射变换过程类似：

<ul> <li > 首先，创建和输入 <spanid="MathJax-Element-91-Frame" tabindex="0"data-mathml="<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>U</mi></math>" role="presentation"><spanid="MathJax-Span-203"><spanid="MathJax-Span-204"><spanid="MathJax-Span-205">U<spanrole="presentation"><math xmlns="http://www.w3.org/1998/Math/MathML"><mi>U</mi></math><script type="math/tex" id="MathJax-Element-91">U</script > 等同空间大小 <spanid="MathJax-Element-92-Frame" tabindex="0"data-mathml="<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">(</mo><mi>H</mi><mo>,</mo><mi>W</mi><mo stretchy="false">)</mo></math>" role="presentation"><spanid="MathJax-Span-206"><spanid="MathJax-Span-207"><spanid="MathJax-Span-208">(<spanid="MathJax-Span-209">H<spanid="MathJax-Span-210">,<spanid="MathJax-Span-211">W<spanid="MathJax-Span-212">)<spanrole="presentation"><math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">(</mo><mi>H</mi><mo>,</mo><mi>W</mi><mo stretchy="false">)</mo></math><script type="math/tex" id="MathJax-Element-92">(H,W)</script > 的棋盘网格 (<spanid="MathJax-Element-93-Frame" tabindex="0"data-mathml="<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">(</mo><msup><mi>x</mi><mi>t</mi></msup><mo>,</mo><msup><mi>y</mi><mi>t</mi></msup><mo stretchy="false">)</mo></math>" role="presentation"><spanid="MathJax-Span-213"><spanid="MathJax-Span-214"><spanid="MathJax-Span-215">(<spanid="MathJax-Span-216"><spanid="MathJax-Span-217">x<spanid="MathJax-Span-218">t<spanid="MathJax-Span-219">,<spanid="MathJax-Span-220"><spanid="MathJax-Span-221">y<spanid="MathJax-Span-222">t<spanid="MathJax-Span-223">)<spanrole="presentation"><math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">(</mo><msup><mi>x</mi><mi>t</mi></msup><mo>,</mo><msup><mi>y</mi><mi>t</mi></msup><mo stretchy="false">)</mo></math><script type="math/tex" id="MathJax-Element-93">(x^t,y^t)</script > 覆盖了所有输入的点，这表示了输出特征中的目标坐标点)</li> <li > 因为我们要在上述创建的棋盘网格做仿射变换，故对上述网格坐标做向量化处理，即 <spanid="MathJax-Element-94-Frame" tabindex="0"data-mathml="<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><mo>[</mo><mtable rowspacing="4pt" columnspacing="1em"><mtr><mtd><msup><mi>x</mi><mi>t</mi></msup><mtext>&#xA0;</mtext><msup><mi>y</mi><mi>t</mi></msup><mtext>&#xA0;</mtext><mn>1</mn></mtd></mtr></mtable><mo>]</mo></mrow></math>" role="presentation"><spanid="MathJax-Span-224"><spanid="MathJax-Span-225"><spanid="MathJax-Span-226"><spanid="MathJax-Span-227">[<spanid="MathJax-Span-228"><spanid="MathJax-Span-229"><spanid="MathJax-Span-230"><spanid="MathJax-Span-231"><spanid="MathJax-Span-232">x<spanid="MathJax-Span-233">t<spanid="MathJax-Span-234"> <spanid="MathJax-Span-235"><spanid="MathJax-Span-236">y<spanid="MathJax-Span-237">t<spanid="MathJax-Span-238"> <spanid="MathJax-Span-239">1<spanid="MathJax-Span-240">]<spanrole="presentation"><math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><mo>[</mo><mtable rowspacing="4pt" columnspacing="1em"><mtr><mtd><msup><mi>x</mi><mi>t</mi></msup><mtext> </mtext><msup><mi>y</mi><mi>t</mi></msup><mtext> </mtext><mn>1</mn></mtd></mtr></mtable><mo>]</mo></mrow></math><script type="math/tex" id="MathJax-Element-94">\begin {bmatrix} x^t \ y^t \ 1 \end {bmatrix}</script > 形式 </li> <li > 将仿射矩阵的参数 reshape 成 <spanid="MathJax-Element-95-Frame" tabindex="0"data-mathml="<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>2</mn><mo>&#xD7;</mo><mn>3</mn></math>" role="presentation"><spanid="MathJax-Span-241"><spanid="MathJax-Span-242"><spanid="MathJax-Span-243">2<spanid="MathJax-Span-244">×<spanid="MathJax-Span-245">3<spanrole="presentation"><math xmlns="http://www.w3.org/1998/Math/MathML"><mn>2</mn><mo>×</mo><mn>3</mn></math><script type="math/tex" id="MathJax-Element-95">2×3</script > 的矩阵形式，并使用下面计算得到我们期望的采样点 </li> </ul>

<div></div><div><spanid="MathJax-Element-96-Frame" tabindex="0"data-mathml="<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"><mrow><mo>(</mo><mtable rowspacing="4pt" columnspacing="1em"><mtr><mtd><msubsup><mi>x</mi><mi>i</mi><mi>s</mi></msubsup></mtd></mtr><mtr><mtd><msubsup><mi>y</mi><mi>i</mi><mi>s</mi></msubsup></mtd></mtr></mtable><mo>)</mo></mrow><mo>=</mo><msub><mi>T</mi><mrow class="MJX-TeXAtom-ORD"><mi>&#x03B8;</mi></mrow></msub><mo stretchy="false">(</mo><msub><mi>G</mi><mi>i</mi></msub><mo stretchy="false">)</mo><mo>=</mo><msub><mi>A</mi><mrow class="MJX-TeXAtom-ORD"><mi>&#x03B8;</mi></mrow></msub><mrow><mo>(</mo><mtable rowspacing="4pt" columnspacing="1em"><mtr><mtd><msubsup><mi>x</mi><mi>i</mi><mi>t</mi></msubsup></mtd></mtr><mtr><mtd><msubsup><mi>y</mi><mi>i</mi><mi>t</mi></msubsup></mtd></mtr><mtr><mtd><mn>1</mn></mtd></mtr></mtable><mo>)</mo></mrow><mo>=</mo><mrow><mo>[</mo><mtable rowspacing="4pt" columnspacing="1em"><mtr><mtd><msub><mi>&#x03B8;</mi><mrow class="MJX-TeXAtom-ORD"><mn>11</mn></mrow></msub></mtd><mtd><msub><mi>&#x03B8;</mi><mrow class="MJX-TeXAtom-ORD"><mn>12</mn></mrow></msub></mtd><mtd><msub><mi>&#x03B8;</mi><mrow class="MJX-TeXAtom-ORD"><mn>13</mn></mrow></msub></mtd></mtr><mtr><mtd><msub><mi>&#x03B8;</mi><mrow class="MJX-TeXAtom-ORD"><mn>21</mn></mrow></msub></mtd><mtd><msub><mi>&#x03B8;</mi><mrow class="MJX-TeXAtom-ORD"><mn>22</mn></mrow></msub></mtd><mtd><msub><mi>&#x03B8;</mi><mrow class="MJX-TeXAtom-ORD"><mn>23</mn></mrow></msub></mtd></mtr></mtable><mo>]</mo></mrow><mrow><mo>(</mo><mtable rowspacing="4pt" columnspacing="1em"><mtr><mtd><msubsup><mi>x</mi><mi>i</mi><mi>t</mi></msubsup></mtd></mtr><mtr><mtd><msubsup><mi>y</mi><mi>i</mi><mi>t</mi></msubsup></mtd></mtr><mtr><mtd><mn>1</mn></mtd></mtr></mtable><mo>)</mo></mrow></math>" role="presentation"><spanid="MathJax-Span-246"><spanid="MathJax-Span-247"><spanid="MathJax-Span-248"><spanid="MathJax-Span-249">(<spanid="MathJax-Span-250"><spanid="MathJax-Span-251"><spanid="MathJax-Span-252"><spanid="MathJax-Span-253"><spanid="MathJax-Span-254">x<spanid="MathJax-Span-255">s<spanid="MathJax-Span-256">i<spanid="MathJax-Span-257"><spanid="MathJax-Span-258"><spanid="MathJax-Span-259"><spanid="MathJax-Span-260">y<spanid="MathJax-Span-261">s<spanid="MathJax-Span-262">i<spanid="MathJax-Span-263">)<spanid="MathJax-Span-264">=<spanid="MathJax-Span-265"><spanid="MathJax-Span-266">T<spanid="MathJax-Span-267"><spanid="MathJax-Span-268"><spanid="MathJax-Span-269">θ<spanid="MathJax-Span-270">(<spanid="MathJax-Span-271"><spanid="MathJax-Span-272">G<spanid="MathJax-Span-273">i<spanid="MathJax-Span-274">)<spanid="MathJax-Span-275">=<spanid="MathJax-Span-276"><spanid="MathJax-Span-277">A<spanid="MathJax-Span-278"><spanid="MathJax-Span-279"><spanid="MathJax-Span-280">θ<spanid="MathJax-Span-281"><spanid="MathJax-Span-282">⎛⎝⎜⎜⎜<spanid="MathJax-Span-283"><spanid="MathJax-Span-284"><spanid="MathJax-Span-285"><spanid="MathJax-Span-286"><spanid="MathJax-Span-287">x<spanid="MathJax-Span-288">t<spanid="MathJax-Span-289">i<spanid="MathJax-Span-290"><spanid="MathJax-Span-291"><spanid="MathJax-Span-292"><spanid="MathJax-Span-293">y<spanid="MathJax-Span-294">t<spanid="MathJax-Span-295">i<spanid="MathJax-Span-296"><spanid="MathJax-Span-297"><spanid="MathJax-Span-298">1<spanid="MathJax-Span-299">⎞⎠⎟⎟⎟<spanid="MathJax-Span-300">=<spanid="MathJax-Span-301"><spanid="MathJax-Span-302">[<spanid="MathJax-Span-303"><spanid="MathJax-Span-304"><spanid="MathJax-Span-305"><spanid="MathJax-Span-306"><spanid="MathJax-Span-307">θ<spanid="MathJax-Span-308"><spanid="MathJax-Span-309"><spanid="MathJax-Span-310">11<spanid="MathJax-Span-325"><spanid="MathJax-Span-326"><spanid="MathJax-Span-327"><spanid="MathJax-Span-328">θ<spanid="MathJax-Span-329"><spanid="MathJax-Span-330"><spanid="MathJax-Span-331">21<spanid="MathJax-Span-311"><spanid="MathJax-Span-312"><spanid="MathJax-Span-313"><spanid="MathJax-Span-314">θ<spanid="MathJax-Span-315"><spanid="MathJax-Span-316"><spanid="MathJax-Span-317">12<spanid="MathJax-Span-332"><spanid="MathJax-Span-333"><spanid="MathJax-Span-334"><spanid="MathJax-Span-335">θ<spanid="MathJax-Span-336"><spanid="MathJax-Span-337"><spanid="MathJax-Span-338">22<spanid="MathJax-Span-318"><spanid="MathJax-Span-319"><spanid="MathJax-Span-320"><spanid="MathJax-Span-321">θ<spanid="MathJax-Span-322"><spanid="MathJax-Span-323"><spanid="MathJax-Span-324">13<spanid="MathJax-Span-339"><spanid="MathJax-Span-340"><spanid="MathJax-Span-341"><spanid="MathJax-Span-342">θ<spanid="MathJax-Span-343"><spanid="MathJax-Span-344"><spanid="MathJax-Span-345">23<spanid="MathJax-Span-346">]<spanid="MathJax-Span-347"><spanid="MathJax-Span-348">⎛⎝⎜⎜⎜<spanid="MathJax-Span-349"><spanid="MathJax-Span-350"><spanid="MathJax-Span-351"><spanid="MathJax-Span-352"><spanid="MathJax-Span-353">x<spanid="MathJax-Span-354">t<spanid="MathJax-Span-355">i<spanid="MathJax-Span-356"><spanid="MathJax-Span-357"><spanid="MathJax-Span-358"><spanid="MathJax-Span-359">y<spanid="MathJax-Span-360">t<spanid="MathJax-Span-361">i<spanid="MathJax-Span-362"><spanid="MathJax-Span-363"><spanid="MathJax-Span-364">1<spanid="MathJax-Span-365">⎞⎠⎟⎟⎟<spanrole="presentation"><math xmlns="http://www.w3.org/1998/Math/MathML" display="block"><mrow><mo>(</mo><mtable rowspacing="4pt" columnspacing="1em"><mtr><mtd><msubsup><mi>x</mi><mi>i</mi><mi>s</mi></msubsup></mtd></mtr><mtr><mtd><msubsup><mi>y</mi><mi>i</mi><mi>s</mi></msubsup></mtd></mtr></mtable><mo>)</mo></mrow><mo>=</mo><msub><mi>T</mi><mrow><mi>θ</mi></mrow></msub><mo stretchy="false">(</mo><msub><mi>G</mi><mi>i</mi></msub><mo stretchy="false">)</mo><mo>=</mo><msub><mi>A</mi><mrow><mi>θ</mi></mrow></msub><mrow><mo>(</mo><mtable rowspacing="4pt" columnspacing="1em"><mtr><mtd><msubsup><mi>x</mi><mi>i</mi><mi>t</mi></msubsup></mtd></mtr><mtr><mtd><msubsup><mi>y</mi><mi>i</mi><mi>t</mi></msubsup></mtd></mtr><mtr><mtd><mn>1</mn></mtd></mtr></mtable><mo>)</mo></mrow><mo>=</mo><mrow><mo>[</mo><mtable rowspacing="4pt" columnspacing="1em"><mtr><mtd><msub><mi>θ</mi><mrow><mn>11</mn></mrow></msub></mtd><mtd><msub><mi>θ</mi><mrow><mn>12</mn></mrow></msub></mtd><mtd><msub><mi>θ</mi><mrow><mn>13</mn></mrow></msub></mtd></mtr><mtr><mtd><msub><mi>θ</mi><mrow><mn>21</mn></mrow></msub></mtd><mtd><msub><mi>θ</mi><mrow><mn>22</mn></mrow></msub></mtd><mtd><msub><mi>θ</mi><mrow><mn>23</mn></mrow></msub></mtd></mtr></mtable><mo>]</mo></mrow><mrow><mo>(</mo><mtable rowspacing="4pt" columnspacing="1em"><mtr><mtd><msubsup><mi>x</mi><mi>i</mi><mi>t</mi></msubsup></mtd></mtr><mtr><mtd><msubsup><mi>y</mi><mi>i</mi><mi>t</mi></msubsup></mtd></mtr><mtr><mtd><mn>1</mn></mtd></mtr></mtable><mo>)</mo></mrow></math></div><script type="math/tex; mode=display" id="MathJax-Element-96">(xsiysi)

=T_{\theta}(G_i) = A_{\theta}

(

[

23]

(

</script>

注意到这里的仿射变换：

如图所示：实际上是通过目标网格找到实际采样网格～

<spanid="MathJax-Element-97-Frame" tabindex="0"data-mathml="<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><mo>[</mo><mtable rowspacing="4pt" columnspacing="1em"><mtr><mtd><msup><mi>x</mi><mi>s</mi></msup><mtext>&#xA0;</mtext><msup><mi>y</mi><mi>s</mi></msup></mtd></mtr></mtable><mo>]</mo></mrow></math>" role="presentation"><spanid="MathJax-Span-366"><spanid="MathJax-Span-367"><spanid="MathJax-Span-368"><spanid="MathJax-Span-369">[<spanid="MathJax-Span-370"><spanid="MathJax-Span-371"><spanid="MathJax-Span-372"><spanid="MathJax-Span-373"><spanid="MathJax-Span-374">x<spanid="MathJax-Span-375">s<spanid="MathJax-Span-376"> <spanid="MathJax-Span-377"><spanid="MathJax-Span-378">y<spanid="MathJax-Span-379">s<spanid="MathJax-Span-380">]<spanrole="presentation"><math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><mo>[</mo><mtable rowspacing="4pt" columnspacing="1em"><mtr><mtd><msup><mi>x</mi><mi>s</mi></msup><mtext> </mtext><msup><mi>y</mi><mi>s</mi></msup></mtd></mtr></mtable><mo>]</mo></mrow></math><script type="math/tex" id="MathJax-Element-97">\begin {bmatrix} x^s \ y^s \end {bmatrix}</script > 表示我们在输入特征上应该采样的点。 想想，上一节我们讲过，如果采样的点是分数该怎么办，是的，使用双线性插值来搞定～

<h2 id="sampler"><a name="t9"></a>Sampler</h2>

注意到， 仿射矩阵参数是可学习的，这要求采样是可微分的，实际中用双线性插值实现仿射变换，刚好双线性插值是可微分的，这刚好符合要求 。

<h3 id="任何采样核"><a name="t10"></a> 任何采样核：</h3>

对于 <spanid="MathJax-Element-98-Frame" tabindex="0"data-mathml="<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">(</mo><msubsup><mi>x</mi><mi>i</mi><mi>s</mi></msubsup><mo>,</mo><msubsup><mi>y</mi><mi>i</mi><mi>s</mi></msubsup><mo stretchy="false">)</mo></math>" role="presentation"><spanid="MathJax-Span-381"><spanid="MathJax-Span-382"><spanid="MathJax-Span-383">(<spanid="MathJax-Span-384"><spanid="MathJax-Span-385">x<spanid="MathJax-Span-386">s<spanid="MathJax-Span-387">i<spanid="MathJax-Span-388">,<spanid="MathJax-Span-389"><spanid="MathJax-Span-390">y<spanid="MathJax-Span-391">s<spanid="MathJax-Span-392">i<spanid="MathJax-Span-393">)<spanrole="presentation"><math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">(</mo><msubsup><mi>x</mi><mi>i</mi><mi>s</mi></msubsup><mo>,</mo><msubsup><mi>y</mi><mi>i</mi><mi>s</mi></msubsup><mo stretchy="false">)</mo></math><script type="math/tex" id="MathJax-Element-98">(x^s_i, y^s_i)</script > 对应的仿射变换 <spanid="MathJax-Element-99-Frame" tabindex="0"data-mathml="<math xmlns="http://www.w3.org/1998/Math/MathML"><msub><mi>T</mi><mrow class="MJX-TeXAtom-ORD"><mi>&#x03B8;</mi></mrow></msub><mo stretchy="false">(</mo><mi>G</mi><mo stretchy="false">)</mo></math>" role="presentation"><spanid="MathJax-Span-394"><spanid="MathJax-Span-395"><spanid="MathJax-Span-396"><spanid="MathJax-Span-397">T<spanid="MathJax-Span-398"><spanid="MathJax-Span-399"><spanid="MathJax-Span-400">θ<spanid="MathJax-Span-401">(<spanid="MathJax-Span-402">G<spanid="MathJax-Span-403">)<spanrole="presentation"><math xmlns="http://www.w3.org/1998/Math/MathML"><msub><mi>T</mi><mrow><mi>θ</mi></mrow></msub><mo stretchy="false">(</mo><mi>G</mi><mo stretchy="false">)</mo></math><script type="math/tex" id="MathJax-Element-99">T_{\theta}(G)</script > 在输入 <spanid="MathJax-Element-100-Frame" tabindex="0"data-mathml="<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>U</mi></math>" role="presentation"><spanid="MathJax-Span-404"><spanid="MathJax-Span-405"><spanid="MathJax-Span-406">U<spanrole="presentation"><math xmlns="http://www.w3.org/1998/Math/MathML"><mi>U</mi></math><script type="math/tex" id="MathJax-Element-100">U</script > 上应用采样核得到输出 <spanid="MathJax-Element-101-Frame" tabindex="0"data-mathml="<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>V</mi></math>" role="presentation"><spanid="MathJax-Span-407"><spanid="MathJax-Span-408"><spanid="MathJax-Span-409">V<spanrole="presentation"><math xmlns="http://www.w3.org/1998/Math/MathML"><mi>V</mi></math><script type="math/tex" id="MathJax-Element-101">V</script>: <div></div><div><spanid="MathJax-Element-102-Frame" tabindex="0"data-mathml="<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"><msubsup><mi>V</mi><mi>c</mi><mi>i</mi></msubsup><mo>=</mo><munderover><mo>&#x2211;</mo><mi>n</mi><mi>H</mi></munderover><munderover><mo>&#x2211;</mo><mi>m</mi><mi>W</mi></munderover><msubsup><mi>U</mi><mrow class="MJX-TeXAtom-ORD"><mi>n</mi><mi>m</mi></mrow><mi>c</mi></msubsup><mi>k</mi><mo stretchy="false">(</mo><msubsup><mi>x</mi><mi>i</mi><mi>s</mi></msubsup><mo>&#x2212;</mo><mi>m</mi><mo>;</mo><msub><mi mathvariant="normal">&#x03A6;</mi><mi>x</mi></msub><mo stretchy="false">)</mo><mi>k</mi><mo stretchy="false">(</mo><msubsup><mi>y</mi><mi>i</mi><mi>s</mi></msubsup><mo>&#x2212;</mo><mi>n</mi><mo>;</mo><msub><mi mathvariant="normal">&#x03A6;</mi><mi>y</mi></msub><mo stretchy="false">)</mo><mtext>&#xA0;</mtext><mtext>&#xA0;</mtext><mi mathvariant="normal">&#x2200;</mi><mi>i</mi><mo>&#x2208;</mo><mo stretchy="false">[</mo><mn>1..</mn><msup><mi>H</mi><mo>&#x2032;</mo></msup><msup><mi>W</mi><mo>&#x2032;</mo></msup><mo stretchy="false">]</mo><mtext>&#xA0;</mtext><mtext>&#xA0;</mtext><mi mathvariant="normal">&#x2200;</mi><mi>c</mi><mo>&#x2208;</mo><mo stretchy="false">[</mo><mn>1..</mn><mi>C</mi><mo stretchy="false">]</mo></math>" role="presentation"><spanid="MathJax-Span-410"><spanid="MathJax-Span-411"><spanid="MathJax-Span-412"><spanid="MathJax-Span-413">V<spanid="MathJax-Span-414">i<spanid="MathJax-Span-415">c<spanid="MathJax-Span-416">=<spanid="MathJax-Span-417"><spanid="MathJax-Span-418">∑<spanid="MathJax-Span-419">n<spanid="MathJax-Span-420">H<spanid="MathJax-Span-421"><spanid="MathJax-Span-422">∑<spanid="MathJax-Span-423">m<spanid="MathJax-Span-424">W<spanid="MathJax-Span-425"><spanid="MathJax-Span-426">U<spanid="MathJax-Span-427">c<spanid="MathJax-Span-428"><spanid="MathJax-Span-429"><spanid="MathJax-Span-430">n<spanid="MathJax-Span-431">m<spanid="MathJax-Span-432">k<spanid="MathJax-Span-433">(<spanid="MathJax-Span-434"><spanid="MathJax-Span-435">x<spanid="MathJax-Span-436">s<spanid="MathJax-Span-437">i<spanid="MathJax-Span-438">−<spanid="MathJax-Span-439">m<spanid="MathJax-Span-440">;<spanid="MathJax-Span-441"><spanid="MathJax-Span-442">Φ<spanid="MathJax-Span-443">x<spanid="MathJax-Span-444">)<spanid="MathJax-Span-445">k<spanid="MathJax-Span-446">(<spanid="MathJax-Span-447"><spanid="MathJax-Span-448">y<spanid="MathJax-Span-449">s<spanid="MathJax-Span-450">i<spanid="MathJax-Span-451">−<spanid="MathJax-Span-452">n<spanid="MathJax-Span-453">;<spanid="MathJax-Span-454"><spanid="MathJax-Span-455">Φ<spanid="MathJax-Span-456">y<spanid="MathJax-Span-457">)<spanid="MathJax-Span-458"> <spanid="MathJax-Span-459"> <spanid="MathJax-Span-460">∀<spanid="MathJax-Span-461">i<spanid="MathJax-Span-462">∈<spanid="MathJax-Span-463">[<spanid="MathJax-Span-464">1..<spanid="MathJax-Span-465"><spanid="MathJax-Span-466">H<spanid="MathJax-Span-467">′<spanid="MathJax-Span-468"><spanid="MathJax-Span-469">W<spanid="MathJax-Span-470">′<spanid="MathJax-Span-471">]<spanid="MathJax-Span-472"> <spanid="MathJax-Span-473"> <spanid="MathJax-Span-474">∀<spanid="MathJax-Span-475">c<spanid="MathJax-Span-476">∈<spanid="MathJax-Span-477">[<spanid="MathJax-Span-478">1..<spanid="MathJax-Span-479">C<spanid="MathJax-Span-480">]<spanrole="presentation"><math xmlns="http://www.w3.org/1998/Math/MathML" display="block"><msubsup><mi>V</mi><mi>c</mi><mi>i</mi></msubsup><mo>=</mo><munderover><mo>∑</mo><mi>n</mi><mi>H</mi></munderover><munderover><mo>∑</mo><mi>m</mi><mi>W</mi></munderover><msubsup><mi>U</mi><mrow><mi>n</mi><mi>m</mi></mrow><mi>c</mi></msubsup><mi>k</mi><mo stretchy="false">(</mo><msubsup><mi>x</mi><mi>i</mi><mi>s</mi></msubsup><mo>−</mo><mi>m</mi><mo>;</mo><msub><mi mathvariant="normal">Φ</mi><mi>x</mi></msub><mo stretchy="false">)</mo><mi>k</mi><mo stretchy="false">(</mo><msubsup><mi>y</mi><mi>i</mi><mi>s</mi></msubsup><mo>−</mo><mi>n</mi><mo>;</mo><msub><mi mathvariant="normal">Φ</mi><mi>y</mi></msub><mo stretchy="false">)</mo><mtext> </mtext><mtext> </mtext><mi mathvariant="normal">∀</mi><mi>i</mi><mo>∈</mo><mo stretchy="false">[</mo><mn>1..</mn><msup><mi>H</mi><mo>′</mo></msup><msup><mi>W</mi><mo>′</mo></msup><mo stretchy="false">]</mo><mtext> </mtext><mtext> </mtext><mi mathvariant="normal">∀</mi><mi>c</mi><mo>∈</mo><mo stretchy="false">[</mo><mn>1..</mn><mi>C</mi><mo stretchy="false">]</mo></math></div><script type="math/tex; mode=display" id="MathJax-Element-102"> V_c^i=\sum^H_n\sum^W_mU^c_{nm} k (x^s_i−m;\Phi_x) k (y^s_i−n;\Phi_y) \ \ \forall i∈[1..H''W''] \ \ \forall c∈[1..C]</script>

其中 <spanid="MathJax-Element-103-Frame" tabindex="0"data-mathml="<math xmlns="http://www.w3.org/1998/Math/MathML"><msub><mi mathvariant="normal">&#x03A6;</mi><mi>x</mi></msub><mo>,</mo><msub><mi mathvariant="normal">&#x03A6;</mi><mi>y</mi></msub></math>" role="presentation"><spanid="MathJax-Span-481"><spanid="MathJax-Span-482"><spanid="MathJax-Span-483"><spanid="MathJax-Span-484">Φ<spanid="MathJax-Span-485">x<spanid="MathJax-Span-486">,<spanid="MathJax-Span-487"><spanid="MathJax-Span-488">Φ<spanid="MathJax-Span-489">y<spanrole="presentation"><math xmlns="http://www.w3.org/1998/Math/MathML"><msub><mi mathvariant="normal">Φ</mi><mi>x</mi></msub><mo>,</mo><msub><mi mathvariant="normal">Φ</mi><mi>y</mi></msub></math><script type="math/tex" id="MathJax-Element-103">\Phi_x,\Phi_y</script > 是采样核 <spanid="MathJax-Element-104-Frame" tabindex="0"data-mathml="<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>k</mi><mo stretchy="false">(</mo><mo stretchy="false">)</mo></math>" role="presentation"><spanid="MathJax-Span-490"><spanid="MathJax-Span-491"><spanid="MathJax-Span-492">k<spanid="MathJax-Span-493">(<spanid="MathJax-Span-494">)<spanrole="presentation"><math xmlns="http://www.w3.org/1998/Math/MathML"><mi>k</mi><mo stretchy="false">(</mo><mo stretchy="false">)</mo></math><script type="math/tex" id="MathJax-Element-104">k ()</script > 的参数，<spanid="MathJax-Element-105-Frame" tabindex="0"data-mathml="<math xmlns="http://www.w3.org/1998/Math/MathML"><msubsup><mi>U</mi><mrow class="MJX-TeXAtom-ORD"><mi>n</mi><mi>m</mi></mrow><mi>c</mi></msubsup></math>" role="presentation"><spanid="MathJax-Span-495"><spanid="MathJax-Span-496"><spanid="MathJax-Span-497"><spanid="MathJax-Span-498">U<spanid="MathJax-Span-499">c<spanid="MathJax-Span-500"><spanid="MathJax-Span-501"><spanid="MathJax-Span-502">n<spanid="MathJax-Span-503">m<spanrole="presentation"><math xmlns="http://www.w3.org/1998/Math/MathML"><msubsup><mi>U</mi><mrow><mi>n</mi><mi>m</mi></mrow><mi>c</mi></msubsup></math><script type="math/tex" id="MathJax-Element-105">U^c_{nm}</script > 在通道 <spanid="MathJax-Element-106-Frame" tabindex="0"data-mathml="<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>c</mi></math>" role="presentation"><spanid="MathJax-Span-504"><spanid="MathJax-Span-505"><spanid="MathJax-Span-506">c<spanrole="presentation"><math xmlns="http://www.w3.org/1998/Math/MathML"><mi>c</mi></math><script type="math/tex" id="MathJax-Element-106">c</script > 上 (n,m) 坐标的值。<spanid="MathJax-Element-107-Frame" tabindex="0"data-mathml="<math xmlns="http://www.w3.org/1998/Math/MathML"><msubsup><mi>V</mi><mi>i</mi><mi>c</mi></msubsup></math>" role="presentation"><spanid="MathJax-Span-507"><spanid="MathJax-Span-508"><spanid="MathJax-Span-509"><spanid="MathJax-Span-510">V<spanid="MathJax-Span-511">c<spanid="MathJax-Span-512">i<spanrole="presentation"><math xmlns="http://www.w3.org/1998/Math/MathML"><msubsup><mi>V</mi><mi>i</mi><mi>c</mi></msubsup></math><script type="math/tex" id="MathJax-Element-107">V^c_i</script > 是像素 <spanid="MathJax-Element-108-Frame" tabindex="0"data-mathml="<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>i</mi></math>" role="presentation"><spanid="MathJax-Span-513"><spanid="MathJax-Span-514"><spanid="MathJax-Span-515">i<spanrole="presentation"><math xmlns="http://www.w3.org/1998/Math/MathML"><mi>i</mi></math><script type="math/tex" id="MathJax-Element-108">i</script > 的输出值，具体指的是通道 <spanid="MathJax-Element-109-Frame" tabindex="0"data-mathml="<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>c</mi></math>" role="presentation"><spanid="MathJax-Span-516"><spanid="MathJax-Span-517"><spanid="MathJax-Span-518">c<spanrole="presentation"><math xmlns="http://www.w3.org/1998/Math/MathML"><mi>c</mi></math><script type="math/tex" id="MathJax-Element-109">c</script > 中位置 <spanid="MathJax-Element-110-Frame" tabindex="0"data-mathml="<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">(</mo><msubsup><mi>x</mi><mi>i</mi><mi>t</mi></msubsup><mo>,</mo><msubsup><mi>y</mi><mi>i</mi><mi>t</mi></msubsup><mo stretchy="false">)</mo></math>" role="presentation"><spanid="MathJax-Span-519"><spanid="MathJax-Span-520"><spanid="MathJax-Span-521">(<spanid="MathJax-Span-522"><spanid="MathJax-Span-523">x<spanid="MathJax-Span-524">t<spanid="MathJax-Span-525">i<spanid="MathJax-Span-526">,<spanid="MathJax-Span-527"><spanid="MathJax-Span-528">y<spanid="MathJax-Span-529">t<spanid="MathJax-Span-530">i<spanid="MathJax-Span-531">)<spanrole="presentation"><math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">(</mo><msubsup><mi>x</mi><mi>i</mi><mi>t</mi></msubsup><mo>,</mo><msubsup><mi>y</mi><mi>i</mi><mi>t</mi></msubsup><mo stretchy="false">)</mo></math><script type="math/tex" id="MathJax-Element-110">(x^t_i,y^t_i)</script>。注意这样的采样应用于每个通道上。

<h3 id="integer-sampling"><a name="t11"></a>integer sampling</h3>

理论上，任何采样核都可以使用，只要可微分即可，即可通过 <spanid="MathJax-Element-111-Frame" tabindex="0"data-mathml="<math xmlns="http://www.w3.org/1998/Math/MathML"><msubsup><mi>x</mi><mi>i</mi><mi>s</mi></msubsup><mo>,</mo><msubsup><mi>y</mi><mi>i</mi><mi>s</mi></msubsup></math>" role="presentation"><spanid="MathJax-Span-532"><spanid="MathJax-Span-533"><spanid="MathJax-Span-534"><spanid="MathJax-Span-535">x<spanid="MathJax-Span-536">s<spanid="MathJax-Span-537">i<spanid="MathJax-Span-538">,<spanid="MathJax-Span-539"><spanid="MathJax-Span-540">y<spanid="MathJax-Span-541">s<spanid="MathJax-Span-542">i<spanrole="presentation"><math xmlns="http://www.w3.org/1998/Math/MathML"><msubsup><mi>x</mi><mi>i</mi><mi>s</mi></msubsup><mo>,</mo><msubsup><mi>y</mi><mi>i</mi><mi>s</mi></msubsup></math><script type="math/tex" id="MathJax-Element-111">x^s_i,y^s_i</script > 定义出梯度，例如使用 integer sampling kernel： <div></div><div><spanid="MathJax-Element-112-Frame" tabindex="0"data-mathml="<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"><msubsup><mi>V</mi><mi>c</mi><mi>i</mi></msubsup><mo>=</mo><munderover><mo>&#x2211;</mo><mi>n</mi><mi>H</mi></munderover><munderover><mo>&#x2211;</mo><mi>m</mi><mi>W</mi></munderover><msubsup><mi>U</mi><mrow class="MJX-TeXAtom-ORD"><mi>n</mi><mi>m</mi></mrow><mi>c</mi></msubsup><mi>&#x03B4;</mi><mo stretchy="false">(</mo><mrow><mo>&#x230A;</mo><mrow><msubsup><mi>x</mi><mi>i</mi><mi>s</mi></msubsup><mo>+</mo><mn>0.5</mn></mrow><mo>&#x230B;</mo></mrow><mo>&#x2212;</mo><mi>m</mi><mo stretchy="false">)</mo><mi>&#x03B4;</mi><mo stretchy="false">(</mo><mrow><mo>&#x230A;</mo><mrow><msubsup><mi>x</mi><mi>i</mi><mi>s</mi></msubsup><mo>+</mo><mn>0.5</mn></mrow><mo>&#x230B;</mo></mrow><mo>&#x2212;</mo><mi>n</mi><mo stretchy="false">)</mo></math>" role="presentation"><spanid="MathJax-Span-543"><spanid="MathJax-Span-544"><spanid="MathJax-Span-545"><spanid="MathJax-Span-546">V<spanid="MathJax-Span-547">i<spanid="MathJax-Span-548">c<spanid="MathJax-Span-549">=<spanid="MathJax-Span-550"><spanid="MathJax-Span-551">∑<spanid="MathJax-Span-552">n<spanid="MathJax-Span-553">H<spanid="MathJax-Span-554"><spanid="MathJax-Span-555">∑<spanid="MathJax-Span-556">m<spanid="MathJax-Span-557">W<spanid="MathJax-Span-558"><spanid="MathJax-Span-559">U<spanid="MathJax-Span-560">c<spanid="MathJax-Span-561"><spanid="MathJax-Span-562"><spanid="MathJax-Span-563">n<spanid="MathJax-Span-564">m<spanid="MathJax-Span-565">δ<spanid="MathJax-Span-566">(<spanid="MathJax-Span-567"><spanid="MathJax-Span-568">⌊<spanid="MathJax-Span-569"><spanid="MathJax-Span-570"><spanid="MathJax-Span-571">x<spanid="MathJax-Span-572">s<spanid="MathJax-Span-573">i<spanid="MathJax-Span-574">+<spanid="MathJax-Span-575">0.5<spanid="MathJax-Span-576">⌋<spanid="MathJax-Span-577">−<spanid="MathJax-Span-578">m<spanid="MathJax-Span-579">)<spanid="MathJax-Span-580">δ<spanid="MathJax-Span-581">(<spanid="MathJax-Span-582"><spanid="MathJax-Span-583">⌊<spanid="MathJax-Span-584"><spanid="MathJax-Span-585"><spanid="MathJax-Span-586">x<spanid="MathJax-Span-587">s<spanid="MathJax-Span-588">i<spanid="MathJax-Span-589">+<spanid="MathJax-Span-590">0.5<spanid="MathJax-Span-591">⌋<spanid="MathJax-Span-592">−<spanid="MathJax-Span-593">n<spanid="MathJax-Span-594">)<spanrole="presentation"><math xmlns="http://www.w3.org/1998/Math/MathML" display="block"><msubsup><mi>V</mi><mi>c</mi><mi>i</mi></msubsup><mo>=</mo><munderover><mo>∑</mo><mi>n</mi><mi>H</mi></munderover><munderover><mo>∑</mo><mi>m</mi><mi>W</mi></munderover><msubsup><mi>U</mi><mrow><mi>n</mi><mi>m</mi></mrow><mi>c</mi></msubsup><mi>δ</mi><mo stretchy="false">(</mo><mrow><mo>⌊</mo><mrow><msubsup><mi>x</mi><mi>i</mi><mi>s</mi></msubsup><mo>+</mo><mn>0.5</mn></mrow><mo>⌋</mo></mrow><mo>−</mo><mi>m</mi><mo stretchy="false">)</mo><mi>δ</mi><mo stretchy="false">(</mo><mrow><mo>⌊</mo><mrow><msubsup><mi>x</mi><mi>i</mi><mi>s</mi></msubsup><mo>+</mo><mn>0.5</mn></mrow><mo>⌋</mo></mrow><mo>−</mo><mi>n</mi><mo stretchy="false">)</mo></math></div><script type="math/tex; mode=display" id="MathJax-Element-112"> V_c^i=\sum^H_n\sum^W_mU^c_{nm}\delta (\left \lfloor x^s_i+0.5 \right \rfloor−m)\delta (\left \lfloor x^s_i+0.5 \right \rfloor−n) </script>

其中 <spanid="MathJax-Element-113-Frame" tabindex="0"data-mathml="<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><mo>&#x230A;</mo><mrow><mi>x</mi><mo>+</mo><mn>0.5</mn></mrow><mo>&#x230B;</mo></mrow></math>" role="presentation"><spanid="MathJax-Span-595"><spanid="MathJax-Span-596"><spanid="MathJax-Span-597"><spanid="MathJax-Span-598">⌊<spanid="MathJax-Span-599"><spanid="MathJax-Span-600">x<spanid="MathJax-Span-601">+<spanid="MathJax-Span-602">0.5<spanid="MathJax-Span-603">⌋<spanrole="presentation"><math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><mo>⌊</mo><mrow><mi>x</mi><mo>+</mo><mn>0.5</mn></mrow><mo>⌋</mo></mrow></math><script type="math/tex" id="MathJax-Element-113">\left \lfloor x+0.5 \right \rfloor</script> 表示 <spanid="MathJax-Element-114-Frame" tabindex="0"data-mathml="<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>x</mi></math>" role="presentation"><spanid="MathJax-Span-604"><spanid="MathJax-Span-605"><spanid="MathJax-Span-606">x<spanrole="presentation"><math xmlns="http://www.w3.org/1998/Math/MathML"><mi>x</mi></math><script type="math/tex" id="MathJax-Element-114">x</script > 最近的整数值，<spanid="MathJax-Element-115-Frame" tabindex="0"data-mathml="<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>&#x03B4;</mi><mo stretchy="false">(</mo><mo stretchy="false">)</mo></math>" role="presentation"><spanid="MathJax-Span-607"><spanid="MathJax-Span-608"><spanid="MathJax-Span-609">δ<spanid="MathJax-Span-610">(<spanid="MathJax-Span-611">)<spanrole="presentation"><math xmlns="http://www.w3.org/1998/Math/MathML"><mi>δ</mi><mo stretchy="false">(</mo><mo stretchy="false">)</mo></math><script type="math/tex" id="MathJax-Element-115">\delta ()</script > 是 Kronecker delta function。这样采样核等同于复制 <spanid="MathJax-Element-116-Frame" tabindex="0"data-mathml="<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">(</mo><msubsup><mi>x</mi><mi>i</mi><mi>s</mi></msubsup><mo>,</mo><msubsup><mi>y</mi><mi>i</mi><mi>s</mi></msubsup><mo stretchy="false">)</mo></math>" role="presentation"><spanid="MathJax-Span-612"><spanid="MathJax-Span-613"><spanid="MathJax-Span-614">(<spanid="MathJax-Span-615"><spanid="MathJax-Span-616">x<spanid="MathJax-Span-617">s<spanid="MathJax-Span-618">i<spanid="MathJax-Span-619">,<spanid="MathJax-Span-620"><spanid="MathJax-Span-621">y<spanid="MathJax-Span-622">s<spanid="MathJax-Span-623">i<spanid="MathJax-Span-624">)<spanrole="presentation"><math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">(</mo><msubsup><mi>x</mi><mi>i</mi><mi>s</mi></msubsup><mo>,</mo><msubsup><mi>y</mi><mi>i</mi><mi>s</mi></msubsup><mo stretchy="false">)</mo></math><script type="math/tex" id="MathJax-Element-116">(x^s_i,y^s_i)</script > 最近的像素值，直接输出为 <spanid="MathJax-Element-117-Frame" tabindex="0"data-mathml="<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">(</mo><msubsup><mi>x</mi><mi>i</mi><mi>t</mi></msubsup><mo>,</mo><msubsup><mi>y</mi><mi>i</mi><mi>t</mi></msubsup><mo stretchy="false">)</mo></math>" role="presentation"><spanid="MathJax-Span-625"><spanid="MathJax-Span-626"><spanid="MathJax-Span-627">(<spanid="MathJax-Span-628"><spanid="MathJax-Span-629">x<spanid="MathJax-Span-630">t<spanid="MathJax-Span-631">i<spanid="MathJax-Span-632">,<spanid="MathJax-Span-633"><spanid="MathJax-Span-634">y<spanid="MathJax-Span-635">t<spanid="MathJax-Span-636">i<spanid="MathJax-Span-637">)<spanrole="presentation"><math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">(</mo><msubsup><mi>x</mi><mi>i</mi><mi>t</mi></msubsup><mo>,</mo><msubsup><mi>y</mi><mi>i</mi><mi>t</mi></msubsup><mo stretchy="false">)</mo></math><script type="math/tex" id="MathJax-Element-117">(x^t_i,y^t_i)</script>。

<h3 id="双线性采样"><a name="t12"></a> 双线性采样 </h3>

对比双线性插值：

<div></div><div><spanid="MathJax-Element-118-Frame" tabindex="0"data-mathml="<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"><mi>f</mi><mo stretchy="false">(</mo><mi>P</mi><mo stretchy="false">)</mo><mo>=</mo><mi>f</mi><mo stretchy="false">(</mo><msub><mi>Q</mi><mrow class="MJX-TeXAtom-ORD"><mn>11</mn></mrow></msub><mo stretchy="false">)</mo><mo stretchy="false">(</mo><msub><mi>x</mi><mn>2</mn></msub><mo>&#x2212;</mo><mi>x</mi><mo stretchy="false">)</mo><mo stretchy="false">(</mo><msub><mi>y</mi><mn>2</mn></msub><mo>&#x2212;</mo><mi>y</mi><mo stretchy="false">)</mo><mo>+</mo><mi>f</mi><mo stretchy="false">(</mo><msub><mi>Q</mi><mrow class="MJX-TeXAtom-ORD"><mn>21</mn></mrow></msub><mo stretchy="false">)</mo><mo stretchy="false">(</mo><mi>x</mi><mo>&#x2212;</mo><msub><mi>x</mi><mn>1</mn></msub><mo stretchy="false">)</mo><mo stretchy="false">(</mo><msub><mi>y</mi><mn>2</mn></msub><mo>&#x2212;</mo><mi>y</mi><mo stretchy="false">)</mo><mo>+</mo><mi>f</mi><mo stretchy="false">(</mo><msub><mi>Q</mi><mrow class="MJX-TeXAtom-ORD"><mn>12</mn></mrow></msub><mo stretchy="false">)</mo><mo stretchy="false">(</mo><msub><mi>x</mi><mn>2</mn></msub><mo>&#x2212;</mo><mi>x</mi><mo stretchy="false">)</mo><mo stretchy="false">(</mo><mi>y</mi><mo>&#x2212;</mo><msub><mi>y</mi><mn>1</mn></msub><mo stretchy="false">)</mo><mo>+</mo><mi>f</mi><mo stretchy="false">(</mo><msub><mi>Q</mi><mrow class="MJX-TeXAtom-ORD"><mn>22</mn></mrow></msub><mo stretchy="false">)</mo><mo stretchy="false">(</mo><mi>x</mi><mo>&#x2212;</mo><msub><mi>x</mi><mn>1</mn></msub><mo stretchy="false">)</mo><mo stretchy="false">(</mo><mi>y</mi><mo>&#x2212;</mo><msub><mi>y</mi><mn>1</mn></msub><mo stretchy="false">)</mo></math>" role="presentation"><spanid="MathJax-Span-638"><spanid="MathJax-Span-639"><spanid="MathJax-Span-640">f<spanid="MathJax-Span-641">(<spanid="MathJax-Span-642">P<spanid="MathJax-Span-643">)<spanid="MathJax-Span-644">=<spanid="MathJax-Span-645">f<spanid="MathJax-Span-646">(<spanid="MathJax-Span-647"><spanid="MathJax-Span-648">Q<spanid="MathJax-Span-649"><spanid="MathJax-Span-650"><spanid="MathJax-Span-651">11<spanid="MathJax-Span-652">)<spanid="MathJax-Span-653">(<spanid="MathJax-Span-654"><spanid="MathJax-Span-655">x<spanid="MathJax-Span-656">2<spanid="MathJax-Span-657">−<spanid="MathJax-Span-658">x<spanid="MathJax-Span-659">)<spanid="MathJax-Span-660">(<spanid="MathJax-Span-661"><spanid="MathJax-Span-662">y<spanid="MathJax-Span-663">2<spanid="MathJax-Span-664">−<spanid="MathJax-Span-665">y<spanid="MathJax-Span-666">)<spanid="MathJax-Span-667">+<spanid="MathJax-Span-668">f<spanid="MathJax-Span-669">(<spanid="MathJax-Span-670"><spanid="MathJax-Span-671">Q<spanid="MathJax-Span-672"><spanid="MathJax-Span-673"><spanid="MathJax-Span-674">21<spanid="MathJax-Span-675">)<spanid="MathJax-Span-676">(<spanid="MathJax-Span-677">x<spanid="MathJax-Span-678">−<spanid="MathJax-Span-679"><spanid="MathJax-Span-680">x<spanid="MathJax-Span-681">1<spanid="MathJax-Span-682">)<spanid="MathJax-Span-683">(<spanid="MathJax-Span-684"><spanid="MathJax-Span-685">y<spanid="MathJax-Span-686">2<spanid="MathJax-Span-687">−<spanid="MathJax-Span-688">y<spanid="MathJax-Span-689">)<spanid="MathJax-Span-690">+<spanid="MathJax-Span-691">f<spanid="MathJax-Span-692">(<spanid="MathJax-Span-693"><spanid="MathJax-Span-694">Q<spanid="MathJax-Span-695"><spanid="MathJax-Span-696"><spanid="MathJax-Span-697">12<spanid="MathJax-Span-698">)<spanid="MathJax-Span-699">(<spanid="MathJax-Span-700"><spanid="MathJax-Span-701">x<spanid="MathJax-Span-702">2<spanid="MathJax-Span-703">−<spanid="MathJax-Span-704">x<spanid="MathJax-Span-705">)<spanid="MathJax-Span-706">(<spanid="MathJax-Span-707">y<spanid="MathJax-Span-708">−<spanid="MathJax-Span-709"><spanid="MathJax-Span-710">y<spanid="MathJax-Span-711">1<spanid="MathJax-Span-712">)<spanid="MathJax-Span-713">+<spanid="MathJax-Span-714">f<spanid="MathJax-Span-715">(<spanid="MathJax-Span-716"><spanid="MathJax-Span-717">Q<spanid="MathJax-Span-718"><spanid="MathJax-Span-719"><spanid="MathJax-Span-720">22<spanid="MathJax-Span-721">)<spanid="MathJax-Span-722">(<spanid="MathJax-Span-723">x<spanid="MathJax-Span-724">−<spanid="MathJax-Span-725"><spanid="MathJax-Span-726">x<spanid="MathJax-Span-727">1<spanid="MathJax-Span-728">)<spanid="MathJax-Span-729">(<spanid="MathJax-Span-730">y<spanid="MathJax-Span-731">−<spanid="MathJax-Span-732"><spanid="MathJax-Span-733">y<spanid="MathJax-Span-734">1<spanid="MathJax-Span-735">)<spanrole="presentation"><math xmlns="http://www.w3.org/1998/Math/MathML" display="block"><mi>f</mi><mo stretchy="false">(</mo><mi>P</mi><mo stretchy="false">)</mo><mo>=</mo><mi>f</mi><mo stretchy="false">(</mo><msub><mi>Q</mi><mrow><mn>11</mn></mrow></msub><mo stretchy="false">)</mo><mo stretchy="false">(</mo><msub><mi>x</mi><mn>2</mn></msub><mo>−</mo><mi>x</mi><mo stretchy="false">)</mo><mo stretchy="false">(</mo><msub><mi>y</mi><mn>2</mn></msub><mo>−</mo><mi>y</mi><mo stretchy="false">)</mo><mo>+</mo><mi>f</mi><mo stretchy="false">(</mo><msub><mi>Q</mi><mrow><mn>21</mn></mrow></msub><mo stretchy="false">)</mo><mo stretchy="false">(</mo><mi>x</mi><mo>−</mo><msub><mi>x</mi><mn>1</mn></msub><mo stretchy="false">)</mo><mo stretchy="false">(</mo><msub><mi>y</mi><mn>2</mn></msub><mo>−</mo><mi>y</mi><mo stretchy="false">)</mo><mo>+</mo><mi>f</mi><mo stretchy="false">(</mo><msub><mi>Q</mi><mrow><mn>12</mn></mrow></msub><mo stretchy="false">)</mo><mo stretchy="false">(</mo><msub><mi>x</mi><mn>2</mn></msub><mo>−</mo><mi>x</mi><mo stretchy="false">)</mo><mo stretchy="false">(</mo><mi>y</mi><mo>−</mo><msub><mi>y</mi><mn>1</mn></msub><mo stretchy="false">)</mo><mo>+</mo><mi>f</mi><mo stretchy="false">(</mo><msub><mi>Q</mi><mrow><mn>22</mn></mrow></msub><mo stretchy="false">)</mo><mo stretchy="false">(</mo><mi>x</mi><mo>−</mo><msub><mi>x</mi><mn>1</mn></msub><mo stretchy="false">)</mo><mo stretchy="false">(</mo><mi>y</mi><mo>−</mo><msub><mi>y</mi><mn>1</mn></msub><mo stretchy="false">)</mo></math></div><script type="math/tex; mode=display" id="MathJax-Element-118">f(P)=f(Q_{11})(x_2-x)(y_2-y)+f(Q_{21})(x-x_1)(y_2-y)+f(Q_{12})(x_2-x)(y-y_1)+f(Q_{22})(x-x_1)(y-y_1) </script>

在 STN 中使用双线性采样核的表达式总结如下：

<div></div><div><spanid="MathJax-Element-119-Frame" tabindex="0"data-mathml="<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"><msubsup><mi>V</mi><mi>c</mi><mi>i</mi></msubsup><mo>=</mo><munderover><mo>&#x2211;</mo><mi>n</mi><mi>H</mi></munderover><munderover><mo>&#x2211;</mo><mi>m</mi><mi>W</mi></munderover><msubsup><mi>U</mi><mrow class="MJX-TeXAtom-ORD"><mi>n</mi><mi>m</mi></mrow><mi>c</mi></msubsup><mo movablelimits="true" form="prefix">max</mo><mo stretchy="false">(</mo><mn>0</mn><mo>,</mo><mn>1</mn><mo>&#x2212;</mo><mrow class="MJX-TeXAtom-ORD"><mo stretchy="false">|</mo></mrow><msubsup><mi>x</mi><mi>i</mi><mi>s</mi></msubsup><mo>&#x2212;</mo><mi>m</mi><mrow class="MJX-TeXAtom-ORD"><mo stretchy="false">|</mo></mrow><mo stretchy="false">)</mo><mo movablelimits="true" form="prefix">max</mo><mo stretchy="false">(</mo><mn>0</mn><mo>,</mo><mn>1</mn><mo>&#x2212;</mo><mrow class="MJX-TeXAtom-ORD"><mo stretchy="false">|</mo></mrow><msubsup><mi>y</mi><mi>i</mi><mi>s</mi></msubsup><mo>&#x2212;</mo><mi>n</mi><mrow class="MJX-TeXAtom-ORD"><mo stretchy="false">|</mo></mrow><mo stretchy="false">)</mo></math>" role="presentation"><spanid="MathJax-Span-736"><spanid="MathJax-Span-737"><spanid="MathJax-Span-738"><spanid="MathJax-Span-739">V<spanid="MathJax-Span-740">i<spanid="MathJax-Span-741">c<spanid="MathJax-Span-742">=<spanid="MathJax-Span-743"><spanid="MathJax-Span-744">∑<spanid="MathJax-Span-745">n<spanid="MathJax-Span-746">H<spanid="MathJax-Span-747"><spanid="MathJax-Span-748">∑<spanid="MathJax-Span-749">m<spanid="MathJax-Span-750">W<spanid="MathJax-Span-751"><spanid="MathJax-Span-752">U<spanid="MathJax-Span-753">c<spanid="MathJax-Span-754"><spanid="MathJax-Span-755"><spanid="MathJax-Span-756">n<spanid="MathJax-Span-757">m<spanid="MathJax-Span-758">max<spanid="MathJax-Span-759">(<spanid="MathJax-Span-760">0<spanid="MathJax-Span-761">,<spanid="MathJax-Span-762">1<spanid="MathJax-Span-763">−<spanid="MathJax-Span-764"><spanid="MathJax-Span-765"><spanid="MathJax-Span-766">|<spanid="MathJax-Span-767"><spanid="MathJax-Span-768">x<spanid="MathJax-Span-769">s<spanid="MathJax-Span-770">i<spanid="MathJax-Span-771">−<spanid="MathJax-Span-772">m<spanid="MathJax-Span-773"><spanid="MathJax-Span-774"><spanid="MathJax-Span-775">|<spanid="MathJax-Span-776">)<spanid="MathJax-Span-777">max<spanid="MathJax-Span-778">(<spanid="MathJax-Span-779">0<spanid="MathJax-Span-780">,<spanid="MathJax-Span-781">1<spanid="MathJax-Span-782">−<spanid="MathJax-Span-783"><spanid="MathJax-Span-784"><spanid="MathJax-Span-785">|<spanid="MathJax-Span-786"><spanid="MathJax-Span-787">y<spanid="MathJax-Span-788">s<spanid="MathJax-Span-789">i<spanid="MathJax-Span-790">−<spanid="MathJax-Span-791">n<spanid="MathJax-Span-792"><spanid="MathJax-Span-793"><spanid="MathJax-Span-794">|<spanid="MathJax-Span-795">)<spanrole="presentation"><math xmlns="http://www.w3.org/1998/Math/MathML" display="block"><msubsup><mi>V</mi><mi>c</mi><mi>i</mi></msubsup><mo>=</mo><munderover><mo>∑</mo><mi>n</mi><mi>H</mi></munderover><munderover><mo>∑</mo><mi>m</mi><mi>W</mi></munderover><msubsup><mi>U</mi><mrow><mi>n</mi><mi>m</mi></mrow><mi>c</mi></msubsup><mo movablelimits="true" form="prefix">max</mo><mo stretchy="false">(</mo><mn>0</mn><mo>,</mo><mn>1</mn><mo>−</mo><mrow><mo stretchy="false">|</mo></mrow><msubsup><mi>x</mi><mi>i</mi><mi>s</mi></msubsup><mo>−</mo><mi>m</mi><mrow><mo stretchy="false">|</mo></mrow><mo stretchy="false">)</mo><mo movablelimits="true" form="prefix">max</mo><mo stretchy="false">(</mo><mn>0</mn><mo>,</mo><mn>1</mn><mo>−</mo><mrow><mo stretchy="false">|</mo></mrow><msubsup><mi>y</mi><mi>i</mi><mi>s</mi></msubsup><mo>−</mo><mi>n</mi><mrow><mo stretchy="false">|</mo></mrow><mo stretchy="false">)</mo></math></div><script type="math/tex; mode=display" id="MathJax-Element-119">V_c^i=\sum^H_n\sum^W_mU^c_{nm}\max(0,1−|x^s_i−m|)\max(0,1−|y^s_i−n|) </script>

这个表达式和双线性插值是一样的。同样是遍历周围的四个点 (上述公式是遍历所有点，实际上是处理点周围的点)，分母省去了，将一堆旁边项目使用 <spanid="MathJax-Element-120-Frame" tabindex="0"data-mathml="<math xmlns="http://www.w3.org/1998/Math/MathML"><mo movablelimits="true" form="prefix">max</mo></math>" role="presentation"><spanid="MathJax-Span-796"><spanid="MathJax-Span-797"><spanid="MathJax-Span-798">max<spanrole="presentation"><math xmlns="http://www.w3.org/1998/Math/MathML"><mo movablelimits="true" form="prefix">max</mo></math><script type="math/tex" id="MathJax-Element-120">\max</script > 函数代替了。

<h3 id="双线性插值的反向传播"><a name="t13"></a > 双线性插值的反向传播 </h3>

这样的双线性插值函数是支持反向传播，我们看看上述双线性采样的偏导数: <div></div><div><spanid="MathJax-Element-121-Frame" tabindex="0"data-mathml="<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"><mtable displaystyle="true"><mlabeledtr><mtd id="mjx-eqn-1"><mtext>(1)</mtext></mtd><mtd><mfrac><mrow><mi mathvariant="normal">&#x2202;</mi><msubsup><mi>V</mi><mi>i</mi><mi>c</mi></msubsup></mrow><mrow><mi mathvariant="normal">&#x2202;</mi><msubsup><mi>U</mi><mrow class="MJX-TeXAtom-ORD"><mi>n</mi><mi>m</mi></mrow><mi>c</mi></msubsup></mrow></mfrac><mo>=</mo><munderover><mo>&#x2211;</mo><mi>n</mi><mi>H</mi></munderover><munderover><mo>&#x2211;</mo><mi>m</mi><mi>W</mi></munderover><mo movablelimits="true" form="prefix">max</mo><mo stretchy="false">(</mo><mn>0</mn><mo>,</mo><mn>1</mn><mo>&#x2212;</mo><mrow class="MJX-TeXAtom-ORD"><mo stretchy="false">|</mo></mrow><msubsup><mi>x</mi><mi>i</mi><mi>s</mi></msubsup><mo>&#x2212;</mo><mi>m</mi><mrow class="MJX-TeXAtom-ORD"><mo stretchy="false">|</mo></mrow><mo stretchy="false">)</mo><mo movablelimits="true" form="prefix">max</mo><mo stretchy="false">(</mo><mn>0</mn><mo>,</mo><mn>1</mn><mo>&#x2212;</mo><mrow class="MJX-TeXAtom-ORD"><mo stretchy="false">|</mo></mrow><msubsup><mi>y</mi><mi>i</mi><mi>s</mi></msubsup><mo>&#x2212;</mo><mi>n</mi><mrow class="MJX-TeXAtom-ORD"><mo stretchy="false">|</mo></mrow><mo stretchy="false">)</mo></mtd></mlabeledtr></mtable></math>" role="presentation"><spanid="MathJax-Span-799"><spanid="MathJax-Span-800"><spanid="MathJax-Span-801"><spanid="MathJax-Span-805"><spanid="MathJax-Span-806"><spanid="MathJax-Span-807"><spanid="MathJax-Span-808"><spanid="MathJax-Span-809">∂<spanid="MathJax-Span-810"><spanid="MathJax-Span-811">V<spanid="MathJax-Span-812">c<spanid="MathJax-Span-813">i<spanid="MathJax-Span-814"><spanid="MathJax-Span-815">∂<spanid="MathJax-Span-816"><spanid="MathJax-Span-817">U<spanid="MathJax-Span-818">c<spanid="MathJax-Span-819"><spanid="MathJax-Span-820"><spanid="MathJax-Span-821">n<spanid="MathJax-Span-822">m<spanid="MathJax-Span-823">=<spanid="MathJax-Span-824"><spanid="MathJax-Span-825">∑<spanid="MathJax-Span-826">n<spanid="MathJax-Span-827">H<spanid="MathJax-Span-828"><spanid="MathJax-Span-829">∑<spanid="MathJax-Span-830">m<spanid="MathJax-Span-831">W<spanid="MathJax-Span-832">max<spanid="MathJax-Span-833">(<spanid="MathJax-Span-834">0<spanid="MathJax-Span-835">,<spanid="MathJax-Span-836">1<spanid="MathJax-Span-837">−<spanid="MathJax-Span-838"><spanid="MathJax-Span-839"><spanid="MathJax-Span-840">|<spanid="MathJax-Span-841"><spanid="MathJax-Span-842">x<spanid="MathJax-Span-843">s<spanid="MathJax-Span-844">i<spanid="MathJax-Span-845">−<spanid="MathJax-Span-846">m<spanid="MathJax-Span-847"><spanid="MathJax-Span-848"><spanid="MathJax-Span-849">|<spanid="MathJax-Span-850">)<spanid="MathJax-Span-851">max<spanid="MathJax-Span-852">(<spanid="MathJax-Span-853">0<spanid="MathJax-Span-854">,<spanid="MathJax-Span-855">1<spanid="MathJax-Span-856">−<spanid="MathJax-Span-857"><spanid="MathJax-Span-858"><spanid="MathJax-Span-859">|<spanid="MathJax-Span-860"><spanid="MathJax-Span-861">y<spanid="MathJax-Span-862">s<spanid="MathJax-Span-863">i<spanid="MathJax-Span-864">−<spanid="MathJax-Span-865">n<spanid="MathJax-Span-866"><spanid="MathJax-Span-867"><spanid="MathJax-Span-868">|<spanid="MathJax-Span-869">)<spanid="mjx-eqn-1"><spanid="MathJax-Span-803"><spanid="MathJax-Span-804">(1)<spanrole="presentation"><math xmlns="http://www.w3.org/1998/Math/MathML" display="block"><mtable display><mlabeledtr><mtd id="mjx-eqn-1"><mtext>(1)</mtext></mtd><mtd><mfrac><mrow><mi mathvariant="normal">∂</mi><msubsup><mi>V</mi><mi>i</mi><mi>c</mi></msubsup></mrow><mrow><mi mathvariant="normal">∂</mi><msubsup><mi>U</mi><mrow><mi>n</mi><mi>m</mi></mrow><mi>c</mi></msubsup></mrow></mfrac><mo>=</mo><munderover><mo>∑</mo><mi>n</mi><mi>H</mi></munderover><munderover><mo>∑</mo><mi>m</mi><mi>W</mi></munderover><mo movablelimits="true" form="prefix">max</mo><mo stretchy="false">(</mo><mn>0</mn><mo>,</mo><mn>1</mn><mo>−</mo><mrow><mo stretchy="false">|</mo></mrow><msubsup><mi>x</mi><mi>i</mi><mi>s</mi></msubsup><mo>−</mo><mi>m</mi><mrow><mo stretchy="false">|</mo></mrow><mo stretchy="false">)</mo><mo movablelimits="true" form="prefix">max</mo><mo stretchy="false">(</mo><mn>0</mn><mo>,</mo><mn>1</mn><mo>−</mo><mrow><mo stretchy="false">|</mo></mrow><msubsup><mi>y</mi><mi>i</mi><mi>s</mi></msubsup><mo>−</mo><mi>n</mi><mrow><mo stretchy="false">|</mo></mrow><mo stretchy="false">)</mo></mtd></mlabeledtr></mtable></math></div><script type="math/tex; mode=display" id="MathJax-Element-121">\frac {\partial V^c_i}{\partial U^c_{nm}}=\sum^H_n\sum^W_m\max (0,1−|x^s_i−m|)\max (0,1−|y^s_i−n|) \tag 1</script>

<div></div><div><spanid="MathJax-Element-122-Frame" tabindex="0"data-mathml="<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"><mtable displaystyle="true"><mlabeledtr><mtd id="mjx-eqn-2"><mtext>(2)</mtext></mtd><mtd><mfrac><mrow><mi mathvariant="normal">&#x2202;</mi><msubsup><mi>V</mi><mi>i</mi><mi>c</mi></msubsup></mrow><mrow><mi mathvariant="normal">&#x2202;</mi><msubsup><mi>x</mi><mrow class="MJX-TeXAtom-ORD"><mi>i</mi></mrow><mi>s</mi></msubsup></mrow></mfrac><mo>=</mo><munderover><mo>&#x2211;</mo><mi>n</mi><mi>H</mi></munderover><munderover><mo>&#x2211;</mo><mi>m</mi><mi>W</mi></munderover><msubsup><mi>U</mi><mrow class="MJX-TeXAtom-ORD"><mi>n</mi><mi>m</mi></mrow><mi>c</mi></msubsup><mo movablelimits="true" form="prefix">max</mo><mo stretchy="false">(</mo><mn>0</mn><mo>,</mo><mn>1</mn><mo>&#x2212;</mo><mrow class="MJX-TeXAtom-ORD"><mo stretchy="false">|</mo></mrow><msubsup><mi>y</mi><mi>i</mi><mi>s</mi></msubsup><mo>&#x2212;</mo><mi>n</mi><mrow class="MJX-TeXAtom-ORD"><mo stretchy="false">|</mo></mrow><mo stretchy="false">)</mo><mo>=</mo><mrow><mo>{</mo><mtable columnalign="left left" rowspacing=".2em" columnspacing="1em" displaystyle="false"><mtr><mtd><mn>0</mn></mtd><mtd><mtext>if&#xA0;</mtext><mrow class="MJX-TeXAtom-ORD"><mo stretchy="false">|</mo></mrow><mi>m</mi><mo>&#x2212;</mo><msubsup><mi>x</mi><mi>i</mi><mi>s</mi></msubsup><mrow class="MJX-TeXAtom-ORD"><mo stretchy="false">|</mo></mrow><mo>&#x2265;</mo><mn>1</mn></mtd></mtr><mtr><mtd><mn>1</mn></mtd><mtd><mtext>if&#xA0;</mtext><mi>m</mi><mo>&#x2265;</mo><msubsup><mi>x</mi><mi>i</mi><mi>s</mi></msubsup></mtd></mtr><mtr><mtd><mo>&#x2212;</mo><mn>1</mn></mtd><mtd><mtext>if&#xA0;</mtext><mi>m</mi><mo>&lt;</mo><msubsup><mi>x</mi><mi>i</mi><mi>s</mi></msubsup></mtd></mtr></mtable><mo fence="true" stretchy="true" symmetric="true"></mo></mrow></mtd></mlabeledtr></mtable></math>" role="presentation"><spanid="MathJax-Span-870"><spanid="MathJax-Span-871"><spanid="MathJax-Span-872"><spanid="MathJax-Span-876"><spanid="MathJax-Span-877"><spanid="MathJax-Span-878"><spanid="MathJax-Span-879"><spanid="MathJax-Span-880">∂<spanid="MathJax-Span-881"><spanid="MathJax-Span-882">V<spanid="MathJax-Span-883">c<spanid="MathJax-Span-884">i<spanid="MathJax-Span-885"><spanid="MathJax-Span-886">∂<spanid="MathJax-Span-887"><spanid="MathJax-Span-888">x<spanid="MathJax-Span-889">s<spanid="MathJax-Span-890"><spanid="MathJax-Span-891"><spanid="MathJax-Span-892">i<spanid="MathJax-Span-893">=<spanid="MathJax-Span-894"><spanid="MathJax-Span-895">∑<spanid="MathJax-Span-896">n<spanid="MathJax-Span-897">H<spanid="MathJax-Span-898"><spanid="MathJax-Span-899">∑<spanid="MathJax-Span-900">m<spanid="MathJax-Span-901">W<spanid="MathJax-Span-902"><spanid="MathJax-Span-903">U<spanid="MathJax-Span-904">c<spanid="MathJax-Span-905"><spanid="MathJax-Span-906"><spanid="MathJax-Span-907">n<spanid="MathJax-Span-908">m<spanid="MathJax-Span-909">max<spanid="MathJax-Span-910">(<spanid="MathJax-Span-911">0<spanid="MathJax-Span-912">,<spanid="MathJax-Span-913">1<spanid="MathJax-Span-914">−<spanid="MathJax-Span-915"><spanid="MathJax-Span-916"><spanid="MathJax-Span-917">|<spanid="MathJax-Span-918"><spanid="MathJax-Span-919">y<spanid="MathJax-Span-920">s<spanid="MathJax-Span-921">i<spanid="MathJax-Span-922">−<spanid="MathJax-Span-923">n<spanid="MathJax-Span-924"><spanid="MathJax-Span-925"><spanid="MathJax-Span-926">|<spanid="MathJax-Span-927">)<spanid="MathJax-Span-928">=<spanid="MathJax-Span-929"><spanid="MathJax-Span-930">⎧⎩⎨⎪⎪<spanid="MathJax-Span-931"><spanid="MathJax-Span-932"><spanid="MathJax-Span-933"><spanid="MathJax-Span-934">0<spanid="MathJax-Span-952"><spanid="MathJax-Span-953"><spanid="MathJax-Span-954">1<spanid="MathJax-Span-964"><spanid="MathJax-Span-965"><spanid="MathJax-Span-966">−<spanid="MathJax-Span-967">1<spanid="MathJax-Span-935"><spanid="MathJax-Span-936"><spanid="MathJax-Span-937">if <spanid="MathJax-Span-938"><spanid="MathJax-Span-939"><spanid="MathJax-Span-940">|<spanid="MathJax-Span-941">m<spanid="MathJax-Span-942">−<spanid="MathJax-Span-943"><spanid="MathJax-Span-944">x<spanid="MathJax-Span-945">s<spanid="MathJax-Span-946">i<spanid="MathJax-Span-947"><spanid="MathJax-Span-948"><spanid="MathJax-Span-949">|<spanid="MathJax-Span-950">≥<spanid="MathJax-Span-951">1<spanid="MathJax-Span-955"><spanid="MathJax-Span-956"><spanid="MathJax-Span-957">if <spanid="MathJax-Span-958">m<spanid="MathJax-Span-959">≥<spanid="MathJax-Span-960"><spanid="MathJax-Span-961">x<spanid="MathJax-Span-962">s<spanid="MathJax-Span-963">i<spanid="MathJax-Span-968"><spanid="MathJax-Span-969"><spanid="MathJax-Span-970">if <spanid="MathJax-Span-971">m<spanid="MathJax-Span-972"><<spanid="MathJax-Span-973"><spanid="MathJax-Span-974">x<spanid="MathJax-Span-975">s<spanid="MathJax-Span-976">i<spanid="MathJax-Span-977"><spanid="mjx-eqn-2"><spanid="MathJax-Span-874"><spanid="MathJax-Span-875">(2)<spanrole="presentation"><math xmlns="http://www.w3.org/1998/Math/MathML" display="block"><mtable display><mlabeledtr><mtd id="mjx-eqn-2"><mtext>(2)</mtext></mtd><mtd><mfrac><mrow><mi mathvariant="normal">∂</mi><msubsup><mi>V</mi><mi>i</mi><mi>c</mi></msubsup></mrow><mrow><mi mathvariant="normal">∂</mi><msubsup><mi>x</mi><mrow><mi>i</mi></mrow><mi>s</mi></msubsup></mrow></mfrac><mo>=</mo><munderover><mo>∑</mo><mi>n</mi><mi>H</mi></munderover><munderover><mo>∑</mo><mi>m</mi><mi>W</mi></munderover><msubsup><mi>U</mi><mrow><mi>n</mi><mi>m</mi></mrow><mi>c</mi></msubsup><mo movablelimits="true" form="prefix">max</mo><mo stretchy="false">(</mo><mn>0</mn><mo>,</mo><mn>1</mn><mo>−</mo><mrow><mo stretchy="false">|</mo></mrow><msubsup><mi>y</mi><mi>i</mi><mi>s</mi></msubsup><mo>−</mo><mi>n</mi><mrow><mo stretchy="false">|</mo></mrow><mo stretchy="false">)</mo><mo>=</mo><mrow><mo>{</mo><mtable columnalign="left left" rowspacing=".2em" columnspacing="1em" display><mtr><mtd><mn>0</mn></mtd><mtd><mtext>if </mtext><mrow><mo stretchy="false">|</mo></mrow><mi>m</mi><mo>−</mo><msubsup><mi>x</mi><mi>i</mi><mi>s</mi></msubsup><mrow><mo stretchy="false">|</mo></mrow><mo>≥</mo><mn>1</mn></mtd></mtr><mtr><mtd><mn>1</mn></mtd><mtd><mtext>if </mtext><mi>m</mi><mo>≥</mo><msubsup><mi>x</mi><mi>i</mi><mi>s</mi></msubsup></mtd></mtr><mtr><mtd><mo>−</mo><mn>1</mn></mtd><mtd><mtext>if </mtext><mi>m</mi><mo><</mo><msubsup><mi>x</mi><mi>i</mi><mi>s</mi></msubsup></mtd></mtr></mtable><mo fence="true" stretchy="true" symmetric="true"></mo></mrow></mtd></mlabeledtr></mtable></math></div><script type="math/tex; mode=display" id="MathJax-Element-122">\frac{\partial V^c_i}{\partial x^s_{i}}=\sum^H_n\sum^W_mU^c_{nm}\max(0,1−|y^s_i−n|) = {0if |m−xsi|≥11if m≥xsi−1if m<xsi

\tag 2</script>

同理 <spanid="MathJax-Element-123-Frame" tabindex="0"data-mathml="<math xmlns="http://www.w3.org/1998/Math/MathML"><mfrac><mrow><mi mathvariant="normal">&#x2202;</mi><msubsup><mi>V</mi><mi>i</mi><mi>c</mi></msubsup></mrow><mrow><mi mathvariant="normal">&#x2202;</mi><msubsup><mi>y</mi><mrow class="MJX-TeXAtom-ORD"><mi>i</mi></mrow><mi>s</mi></msubsup></mrow></mfrac></math>" role="presentation"><spanid="MathJax-Span-978"><spanid="MathJax-Span-979"><spanid="MathJax-Span-980"><spanid="MathJax-Span-981"><spanid="MathJax-Span-982">∂<spanid="MathJax-Span-983"><spanid="MathJax-Span-984">V<spanid="MathJax-Span-985">c<spanid="MathJax-Span-986">i<spanid="MathJax-Span-987"><spanid="MathJax-Span-988">∂<spanid="MathJax-Span-989"><spanid="MathJax-Span-990">y<spanid="MathJax-Span-991">s<spanid="MathJax-Span-992"><spanid="MathJax-Span-993"><spanid="MathJax-Span-994">i<spanrole="presentation"><math xmlns="http://www.w3.org/1998/Math/MathML"><mfrac><mrow><mi mathvariant="normal">∂</mi><msubsup><mi>V</mi><mi>i</mi><mi>c</mi></msubsup></mrow><mrow><mi mathvariant="normal">∂</mi><msubsup><mi>y</mi><mrow><mi>i</mi></mrow><mi>s</mi></msubsup></mrow></mfrac></math><script type="math/tex" id="MathJax-Element-123">\frac {\partial V^c_i}{\partial y^s_{i}}</script > 类似。

双线性插值支持微分操作，允许梯度流回传到 feature map 上 (2)，并且回传到采样坐标上 (1)，这样就能调整学习到的变换参数 <spanid="MathJax-Element-124-Frame" tabindex="0"data-mathml="<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>&#x03B8;</mi></math>" role="presentation"><spanid="MathJax-Span-995"><spanid="MathJax-Span-996"><spanid="MathJax-Span-997">θ<spanrole="presentation"><math xmlns="http://www.w3.org/1998/Math/MathML"><mi>θ</mi></math><script type="math/tex" id="MathJax-Element-124">\theta</script>，因为 < code>localisation net</code > 中 <spanid="MathJax-Element-125-Frame" tabindex="0"data-mathml="<math xmlns="http://www.w3.org/1998/Math/MathML"><mfrac><mrow><mi mathvariant="normal">&#x2202;</mi><msubsup><mi>x</mi><mi>i</mi><mi>s</mi></msubsup></mrow><mrow><mi mathvariant="normal">&#x2202;</mi><mi>&#x03B8;</mi></mrow></mfrac></math>" role="presentation"><spanid="MathJax-Span-998"><spanid="MathJax-Span-999"><spanid="MathJax-Span-1000"><spanid="MathJax-Span-1001"><spanid="MathJax-Span-1002">∂<spanid="MathJax-Span-1003"><spanid="MathJax-Span-1004">x<spanid="MathJax-Span-1005">s<spanid="MathJax-Span-1006">i<spanid="MathJax-Span-1007"><spanid="MathJax-Span-1008">∂<spanid="MathJax-Span-1009">θ<spanrole="presentation"><math xmlns="http://www.w3.org/1998/Math/MathML"><mfrac><mrow><mi mathvariant="normal">∂</mi><msubsup><mi>x</mi><mi>i</mi><mi>s</mi></msubsup></mrow><mrow><mi mathvariant="normal">∂</mi><mi>θ</mi></mrow></mfrac></math><script type="math/tex" id="MathJax-Element-125">\frac {\partial x^s_i}{\partial \theta}</script > 和 <spanid="MathJax-Element-126-Frame" tabindex="0"data-mathml="<math xmlns="http://www.w3.org/1998/Math/MathML"><mfrac><mrow><mi mathvariant="normal">&#x2202;</mi><msubsup><mi>y</mi><mi>i</mi><mi>s</mi></msubsup></mrow><mrow><mi mathvariant="normal">&#x2202;</mi><mi>&#x03B8;</mi></mrow></mfrac></math>" role="presentation"><spanid="MathJax-Span-1010"><spanid="MathJax-Span-1011"><spanid="MathJax-Span-1012"><spanid="MathJax-Span-1013"><spanid="MathJax-Span-1014">∂<spanid="MathJax-Span-1015"><spanid="MathJax-Span-1016">y<spanid="MathJax-Span-1017">s<spanid="MathJax-Span-1018">i<spanid="MathJax-Span-1019"><spanid="MathJax-Span-1020">∂<spanid="MathJax-Span-1021">θ<spanrole="presentation"><math xmlns="http://www.w3.org/1998/Math/MathML"><mfrac><mrow><mi mathvariant="normal">∂</mi><msubsup><mi>y</mi><mi>i</mi><mi>s</mi></msubsup></mrow><mrow><mi mathvariant="normal">∂</mi><mi>θ</mi></mrow></mfrac></math><script type="math/tex" id="MathJax-Element-126">\frac {\partial y^s_i}{\partial \theta}</script > 可帮助修正矩阵。示意图如下：

双线性采样实现了整个 BP，注意上述的公式是迭代所有输入位置，实际操作是指看周围的像素点。

在输入 <spanid="MathJax-Element-127-Frame" tabindex="0"data-mathml="<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>U</mi></math>" role="presentation"><spanid="MathJax-Span-1022"><spanid="MathJax-Span-1023"><spanid="MathJax-Span-1024">U<spanrole="presentation"><math xmlns="http://www.w3.org/1998/Math/MathML"><mi>U</mi></math><script type="math/tex" id="MathJax-Element-127">U</script > 上双线性采样得到 shape 为 <spanid="MathJax-Element-128-Frame" tabindex="0"data-mathml="<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">(</mo><msup><mi>H</mi><mo>&#x2032;</mo></msup><mo>,</mo><msup><mi>W</mi><mo>&#x2032;</mo></msup><mo>,</mo><msup><mi>C</mi><mo>&#x2032;</mo></msup><mo stretchy="false">)</mo></math>" role="presentation"><spanid="MathJax-Span-1025"><spanid="MathJax-Span-1026"><spanid="MathJax-Span-1027">(<spanid="MathJax-Span-1028"><spanid="MathJax-Span-1029">H<spanid="MathJax-Span-1030">′<spanid="MathJax-Span-1031">,<spanid="MathJax-Span-1032"><spanid="MathJax-Span-1033">W<spanid="MathJax-Span-1034">′<spanid="MathJax-Span-1035">,<spanid="MathJax-Span-1036"><spanid="MathJax-Span-1037">C<spanid="MathJax-Span-1038">′<spanid="MathJax-Span-1039">)<spanrole="presentation"><math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">(</mo><msup><mi>H</mi><mo>′</mo></msup><mo>,</mo><msup><mi>W</mi><mo>′</mo></msup><mo>,</mo><msup><mi>C</mi><mo>′</mo></msup><mo stretchy="false">)</mo></math><script type="math/tex" id="MathJax-Element-128">(H'',W'',C'')</script > 的输出 <spanid="MathJax-Element-129-Frame" tabindex="0"data-mathml="<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>V</mi></math>" role="presentation"><spanid="MathJax-Span-1040"><spanid="MathJax-Span-1041"><spanid="MathJax-Span-1042">V<spanrole="presentation"><math xmlns="http://www.w3.org/1998/Math/MathML"><mi>V</mi></math><script type="math/tex" id="MathJax-Element-129">V</script>, 这意味着我们可以指定 shape 大小，达到上采样或下采样的目的。我们的设计不受限于双线性采样，其他的采样核也可以使用，重要的是支持可微分，这样才能反向传播训练 < code>localisation net</code>。

<h2 id="空间变换案例"><a name="t14"></a > 空间变换案例 </h2>

<h3 id="distorted-mnist"><a name="t15"></a>Distorted MNIST</h3>

在 Disturted MNIST 上使用空间变换得到的结果：

可以看到这是如何精准的学习到健壮的分类模型，通过放缩和消除背景影响，定位的关键信息，再做标准化操作。

<h3 id="german-traffic-sign-recognition-benchmark-gtsrb-dataset"><a name="t16"></a>German Traffic Sign Recognition Benchmark (GTSRB) dataset</h3>

可以看到空间变换集中于关键信息上，移除了背景信息。

<a href="http://pdfs.semanticscholar.org/31c1/9d90cb4f56794e40fedda9fa73e9eecec178.pdf" rel="nofollow" target="_blank">Spatial Transformer Networks</a>

<hr>

<h1 id="常见的仿射变换"><a name="t18"></a > 常见的仿射变换 </h1>

<ul> <li> 平移变换： <div></div><div><spanid="MathJax-Element-72-Frame" tabindex="0"data-mathml="<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"><mrow><mo>[</mo><mtable rowspacing="4pt" columnspacing="1em"><mtr><mtd><mn>1</mn></mtd><mtd><mn>0</mn></mtd><mtd><msub><mi>&#x03B8;</mi><mrow class="MJX-TeXAtom-ORD"><mn>13</mn></mrow></msub></mtd></mtr><mtr><mtd><mn>0</mn></mtd><mtd><mn>1</mn></mtd><mtd><msub><mi>&#x03B8;</mi><mrow class="MJX-TeXAtom-ORD"><mn>23</mn></mrow></msub></mtd></mtr></mtable><mo>]</mo></mrow><mrow><mo>(</mo><mtable rowspacing="4pt" columnspacing="1em"><mtr><mtd><msubsup><mi>x</mi><mi>i</mi><mi>t</mi></msubsup></mtd></mtr><mtr><mtd><msubsup><mi>y</mi><mi>i</mi><mi>t</mi></msubsup></mtd></mtr><mtr><mtd><mn>1</mn></mtd></mtr></mtable><mo>)</mo></mrow><mo>=</mo><mrow><mo>(</mo><mtable rowspacing="4pt" columnspacing="1em"><mtr><mtd><msubsup><mi>x</mi><mi>i</mi><mi>t</mi></msubsup><mo>+</mo><msub><mi>&#x03B8;</mi><mrow class="MJX-TeXAtom-ORD"><mn>13</mn></mrow></msub></mtd></mtr><mtr><mtd><msubsup><mi>y</mi><mi>i</mi><mi>t</mi></msubsup><mo>+</mo><msub><mi>&#x03B8;</mi><mrow class="MJX-TeXAtom-ORD"><mn>23</mn></mrow></msub></mtd></mtr></mtable><mo>)</mo></mrow></math>" role="presentation"><spanid="MathJax-Span-1043"><spanid="MathJax-Span-1044"><spanid="MathJax-Span-1045"><spanid="MathJax-Span-1046">[<spanid="MathJax-Span-1047"><spanid="MathJax-Span-1048"><spanid="MathJax-Span-1049"><spanid="MathJax-Span-1050">1<spanid="MathJax-Span-1061"><spanid="MathJax-Span-1062"><spanid="MathJax-Span-1063">0<spanid="MathJax-Span-1051"><spanid="MathJax-Span-1052"><spanid="MathJax-Span-1053">0<spanid="MathJax-Span-1064"><spanid="MathJax-Span-1065"><spanid="MathJax-Span-1066">1<spanid="MathJax-Span-1054"><spanid="MathJax-Span-1055"><spanid="MathJax-Span-1056"><spanid="MathJax-Span-1057">θ<spanid="MathJax-Span-1058"><spanid="MathJax-Span-1059"><spanid="MathJax-Span-1060">13<spanid="MathJax-Span-1067"><spanid="MathJax-Span-1068"><spanid="MathJax-Span-1069"><spanid="MathJax-Span-1070">θ<spanid="MathJax-Span-1071"><spanid="MathJax-Span-1072"><spanid="MathJax-Span-1073">23<spanid="MathJax-Span-1074">]<spanid="MathJax-Span-1075"><spanid="MathJax-Span-1076">⎛⎝⎜⎜⎜<spanid="MathJax-Span-1077"><spanid="MathJax-Span-1078"><spanid="MathJax-Span-1079"><spanid="MathJax-Span-1080"><spanid="MathJax-Span-1081">x<spanid="MathJax-Span-1082">t<spanid="MathJax-Span-1083">i<spanid="MathJax-Span-1084"><spanid="MathJax-Span-1085"><spanid="MathJax-Span-1086"><spanid="MathJax-Span-1087">y<spanid="MathJax-Span-1088">t<spanid="MathJax-Span-1089">i<spanid="MathJax-Span-1090"><spanid="MathJax-Span-1091"><spanid="MathJax-Span-1092">1<spanid="MathJax-Span-1093">⎞⎠⎟⎟⎟<spanid="MathJax-Span-1094">=<spanid="MathJax-Span-1095"><spanid="MathJax-Span-1096">(<spanid="MathJax-Span-1097"><spanid="MathJax-Span-1098"><spanid="MathJax-Span-1099"><spanid="MathJax-Span-1100"><spanid="MathJax-Span-1101">x<spanid="MathJax-Span-1102">t<spanid="MathJax-Span-1103">i<spanid="MathJax-Span-1104">+<spanid="MathJax-Span-1105"><spanid="MathJax-Span-1106">θ<spanid="MathJax-Span-1107"><spanid="MathJax-Span-1108"><spanid="MathJax-Span-1109">13<spanid="MathJax-Span-1110"><spanid="MathJax-Span-1111"><spanid="MathJax-Span-1112"><spanid="MathJax-Span-1113">y<spanid="MathJax-Span-1114">t<spanid="MathJax-Span-1115">i<spanid="MathJax-Span-1116">+<spanid="MathJax-Span-1117"><spanid="MathJax-Span-1118">θ<spanid="MathJax-Span-1119"><spanid="MathJax-Span-1120"><spanid="MathJax-Span-1121">23<spanid="MathJax-Span-1122">)<spanrole="presentation"><math xmlns="http://www.w3.org/1998/Math/MathML" display="block"><mrow><mo>[</mo><mtable rowspacing="4pt" columnspacing="1em"><mtr><mtd><mn>1</mn></mtd><mtd><mn>0</mn></mtd><mtd><msub><mi>θ</mi><mrow><mn>13</mn></mrow></msub></mtd></mtr><mtr><mtd><mn>0</mn></mtd><mtd><mn>1</mn></mtd><mtd><msub><mi>θ</mi><mrow><mn>23</mn></mrow></msub></mtd></mtr></mtable><mo>]</mo></mrow><mrow><mo>(</mo><mtable rowspacing="4pt" columnspacing="1em"><mtr><mtd><msubsup><mi>x</mi><mi>i</mi><mi>t</mi></msubsup></mtd></mtr><mtr><mtd><msubsup><mi>y</mi><mi>i</mi><mi>t</mi></msubsup></mtd></mtr><mtr><mtd><mn>1</mn></mtd></mtr></mtable><mo>)</mo></mrow><mo>=</mo><mrow><mo>(</mo><mtable rowspacing="4pt" columnspacing="1em"><mtr><mtd><msubsup><mi>x</mi><mi>i</mi><mi>t</mi></msubsup><mo>+</mo><msub><mi>θ</mi><mrow><mn>13</mn></mrow></msub></mtd></mtr><mtr><mtd><msubsup><mi>y</mi><mi>i</mi><mi>t</mi></msubsup><mo>+</mo><msub><mi>θ</mi><mrow><mn>23</mn></mrow></msub></mtd></mtr></mtable><mo>)</mo></mrow></math></div><script type="math/tex; mode=display" id="MathJax-Element-72">\begin {bmatrix} 1& 0 &\theta_{13} \\ 0&1 & \theta_{23} \end {bmatrix} \begin {pmatrix} x_i^t\\ y_i^t \\ 1 \end {pmatrix} =\begin {pmatrix} x_i^t+\theta_{13}\\ y_i^t+\theta_{23} \end {pmatrix}</script></li> <li> 缩放变换： <div></div><div><spanid="MathJax-Element-73-Frame" tabindex="0"data-mathml="<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"><mrow><mo>[</mo><mtable rowspacing="4pt" columnspacing="1em"><mtr><mtd><msub><mi>&#x03B8;</mi><mrow class="MJX-TeXAtom-ORD"><mn>11</mn></mrow></msub></mtd><mtd><mn>0</mn></mtd><mtd><mn>0</mn></mtd></mtr><mtr><mtd><mn>0</mn></mtd><mtd><msub><mi>&#x03B8;</mi><mrow class="MJX-TeXAtom-ORD"><mn>12</mn></mrow></msub></mtd><mtd><mn>0</mn></mtd></mtr></mtable><mo>]</mo></mrow><mrow><mo>(</mo><mtable rowspacing="4pt" columnspacing="1em"><mtr><mtd><msubsup><mi>x</mi><mi>i</mi><mi>t</mi></msubsup></mtd></mtr><mtr><mtd><msubsup><mi>y</mi><mi>i</mi><mi>t</mi></msubsup></mtd></mtr><mtr><mtd><mn>1</mn></mtd></mtr></mtable><mo>)</mo></mrow><mo>=</mo><mrow><mo>(</mo><mtable rowspacing="4pt" columnspacing="1em"><mtr><mtd><msub><mi>&#x03B8;</mi><mrow class="MJX-TeXAtom-ORD"><mn>11</mn></mrow></msub><msubsup><mi>x</mi><mi>i</mi><mi>t</mi></msubsup></mtd></mtr><mtr><mtd><msub><mi>&#x03B8;</mi><mrow class="MJX-TeXAtom-ORD"><mn>12</mn></mrow></msub><msubsup><mi>y</mi><mi>i</mi><mi>t</mi></msubsup></mtd></mtr></mtable><mo>)</mo></mrow></math>" role="presentation"><spanid="MathJax-Span-1123"><spanid="MathJax-Span-1124"><spanid="MathJax-Span-1125"><spanid="MathJax-Span-1126">[<spanid="MathJax-Span-1127"><spanid="MathJax-Span-1128"><spanid="MathJax-Span-1129"><spanid="MathJax-Span-1130"><spanid="MathJax-Span-1131">θ<spanid="MathJax-Span-1132"><spanid="MathJax-Span-1133"><spanid="MathJax-Span-1134">11<spanid="MathJax-Span-1141"><spanid="MathJax-Span-1142"><spanid="MathJax-Span-1143">0<spanid="MathJax-Span-1135"><spanid="MathJax-Span-1136"><spanid="MathJax-Span-1137">0<spanid="MathJax-Span-1144"><spanid="MathJax-Span-1145"><spanid="MathJax-Span-1146"><spanid="MathJax-Span-1147">θ<spanid="MathJax-Span-1148"><spanid="MathJax-Span-1149"><spanid="MathJax-Span-1150">12<spanid="MathJax-Span-1138"><spanid="MathJax-Span-1139"><spanid="MathJax-Span-1140">0<spanid="MathJax-Span-1151"><spanid="MathJax-Span-1152"><spanid="MathJax-Span-1153">0<spanid="MathJax-Span-1154">]<spanid="MathJax-Span-1155"><spanid="MathJax-Span-1156">⎛⎝⎜⎜⎜<spanid="MathJax-Span-1157"><spanid="MathJax-Span-1158"><spanid="MathJax-Span-1159"><spanid="MathJax-Span-1160"><spanid="MathJax-Span-1161">x<spanid="MathJax-Span-1162">t<spanid="MathJax-Span-1163">i<spanid="MathJax-Span-1164"><spanid="MathJax-Span-1165"><spanid="MathJax-Span-1166"><spanid="MathJax-Span-1167">y<spanid="MathJax-Span-1168">t<spanid="MathJax-Span-1169">i<spanid="MathJax-Span-1170"><spanid="MathJax-Span-1171"><spanid="MathJax-Span-1172">1<spanid="MathJax-Span-1173">⎞⎠⎟⎟⎟<spanid="MathJax-Span-1174">=<spanid="MathJax-Span-1175"><spanid="MathJax-Span-1176">(<spanid="MathJax-Span-1177"><spanid="MathJax-Span-1178"><spanid="MathJax-Span-1179"><spanid="MathJax-Span-1180"><spanid="MathJax-Span-1181">θ<spanid="MathJax-Span-1182"><spanid="MathJax-Span-1183"><spanid="MathJax-Span-1184">11<spanid="MathJax-Span-1185"><spanid="MathJax-Span-1186">x<spanid="MathJax-Span-1187">t<spanid="MathJax-Span-1188">i<spanid="MathJax-Span-1189"><spanid="MathJax-Span-1190"><spanid="MathJax-Span-1191"><spanid="MathJax-Span-1192">θ<spanid="MathJax-Span-1193"><spanid="MathJax-Span-1194"><spanid="MathJax-Span-1195">12<spanid="MathJax-Span-1196"><spanid="MathJax-Span-1197">y<spanid="MathJax-Span-1198">t<spanid="MathJax-Span-1199">i<spanid="MathJax-Span-1200">)<spanrole="presentation"><math xmlns="http://www.w3.org/1998/Math/MathML" display="block"><mrow><mo>[</mo><mtable rowspacing="4pt" columnspacing="1em"><mtr><mtd><msub><mi>θ</mi><mrow><mn>11</mn></mrow></msub></mtd><mtd><mn>0</mn></mtd><mtd><mn>0</mn></mtd></mtr><mtr><mtd><mn>0</mn></mtd><mtd><msub><mi>θ</mi><mrow><mn>12</mn></mrow></msub></mtd><mtd><mn>0</mn></mtd></mtr></mtable><mo>]</mo></mrow><mrow><mo>(</mo><mtable rowspacing="4pt" columnspacing="1em"><mtr><mtd><msubsup><mi>x</mi><mi>i</mi><mi>t</mi></msubsup></mtd></mtr><mtr><mtd><msubsup><mi>y</mi><mi>i</mi><mi>t</mi></msubsup></mtd></mtr><mtr><mtd><mn>1</mn></mtd></mtr></mtable><mo>)</mo></mrow><mo>=</mo><mrow><mo>(</mo><mtable rowspacing="4pt" columnspacing="1em"><mtr><mtd><msub><mi>θ</mi><mrow><mn>11</mn></mrow></msub><msubsup><mi>x</mi><mi>i</mi><mi>t</mi></msubsup></mtd></mtr><mtr><mtd><msub><mi>θ</mi><mrow><mn>12</mn></mrow></msub><msubsup><mi>y</mi><mi>i</mi><mi>t</mi></msubsup></mtd></mtr></mtable><mo>)</mo></mrow></math></div><script type="math/tex; mode=display" id="MathJax-Element-73">\begin {bmatrix} \theta_{11}& 0 &0 \\ 0&\theta_{12} & 0 \end {bmatrix} \begin {pmatrix} x_i^t\\ y_i^t \\ 1 \end {pmatrix} =\begin {pmatrix} \theta_{11} x_i^t\\ \theta_{12} y_i^t \end {pmatrix}</script></li> <li> 旋转操作： <div></div><div><spanid="MathJax-Element-74-Frame" tabindex="0"data-mathml="<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"><mrow><mo>[</mo><mtable rowspacing="4pt" columnspacing="1em"><mtr><mtd><mi>cos</mi><mo>&#x2061;</mo><mo stretchy="false">(</mo><mi>&#x03B1;</mi><mo stretchy="false">)</mo></mtd><mtd><mi>sin</mi><mo>&#x2061;</mo><mo stretchy="false">(</mo><mi>&#x03B1;</mi><mo stretchy="false">)</mo></mtd><mtd><mn>0</mn></mtd></mtr><mtr><mtd><mo>&#x2212;</mo><mi>sin</mi><mo>&#x2061;</mo><mo stretchy="false">(</mo><mi>&#x03B1;</mi><mo stretchy="false">)</mo></mtd><mtd><mi>cos</mi><mo>&#x2061;</mo><mo stretchy="false">(</mo><mi>&#x03B1;</mi><mo stretchy="false">)</mo></mtd><mtd><mn>0</mn></mtd></mtr></mtable><mo>]</mo></mrow><mrow><mo>(</mo><mtable rowspacing="4pt" columnspacing="1em"><mtr><mtd><msubsup><mi>x</mi><mi>i</mi><mi>t</mi></msubsup></mtd></mtr><mtr><mtd><msubsup><mi>y</mi><mi>i</mi><mi>t</mi></msubsup></mtd></mtr><mtr><mtd><mn>1</mn></mtd></mtr></mtable><mo>)</mo></mrow><mo>=</mo><mrow><mo>(</mo><mtable rowspacing="4pt" columnspacing="1em"><mtr><mtd><mi>cos</mi><mo>&#x2061;</mo><mo stretchy="false">(</mo><mi>&#x03B1;</mi><mo stretchy="false">)</mo><msubsup><mi>x</mi><mi>i</mi><mi>t</mi></msubsup><mo>+</mo><mi>sin</mi><mo>&#x2061;</mo><mo stretchy="false">(</mo><mi>&#x03B1;</mi><mo stretchy="false">)</mo><msubsup><mi>y</mi><mi>i</mi><mi>t</mi></msubsup></mtd></mtr><mtr><mtd><mo>&#x2212;</mo><mi>sin</mi><mo>&#x2061;</mo><mo stretchy="false">(</mo><mi>&#x03B1;</mi><mo stretchy="false">)</mo><msubsup><mi>x</mi><mi>i</mi><mi>t</mi></msubsup><mo>+</mo><mi>cos</mi><mo>&#x2061;</mo><mo stretchy="false">(</mo><mi>&#x03B1;</mi><mo stretchy="false">)</mo><msubsup><mi>y</mi><mi>i</mi><mi>t</mi></msubsup></mtd></mtr></mtable><mo>)</mo></mrow></math>" role="presentation"><spanid="MathJax-Span-1201"><spanid="MathJax-Span-1202"><spanid="MathJax-Span-1203"><spanid="MathJax-Span-1204">[<spanid="MathJax-Span-1205"><spanid="MathJax-Span-1206"><spanid="MathJax-Span-1207"><spanid="MathJax-Span-1208">cos<spanid="MathJax-Span-1209"><spanid="MathJax-Span-1210">(<spanid="MathJax-Span-1211">α<spanid="MathJax-Span-1212">)<spanid="MathJax-Span-1223"><spanid="MathJax-Span-1224"><spanid="MathJax-Span-1225">−<spanid="MathJax-Span-1226">sin<spanid="MathJax-Span-1227"><spanid="MathJax-Span-1228">(<spanid="MathJax-Span-1229">α<spanid="MathJax-Span-1230">)<spanid="MathJax-Span-1213"><spanid="MathJax-Span-1214"><spanid="MathJax-Span-1215">sin<spanid="MathJax-Span-1216"><spanid="MathJax-Span-1217">(<spanid="MathJax-Span-1218">α<spanid="MathJax-Span-1219">)<spanid="MathJax-Span-1231"><spanid="MathJax-Span-1232"><spanid="MathJax-Span-1233">cos<spanid="MathJax-Span-1234"><spanid="MathJax-Span-1235">(<spanid="MathJax-Span-1236">α<spanid="MathJax-Span-1237">)<spanid="MathJax-Span-1220"><spanid="MathJax-Span-1221"><spanid="MathJax-Span-1222">0<spanid="MathJax-Span-1238"><spanid="MathJax-Span-1239"><spanid="MathJax-Span-1240">0<spanid="MathJax-Span-1241">]<spanid="MathJax-Span-1242"><spanid="MathJax-Span-1243">⎛⎝⎜⎜⎜<spanid="MathJax-Span-1244"><spanid="MathJax-Span-1245"><spanid="MathJax-Span-1246"><spanid="MathJax-Span-1247"><spanid="MathJax-Span-1248">x<spanid="MathJax-Span-1249">t<spanid="MathJax-Span-1250">i<spanid="MathJax-Span-1251"><spanid="MathJax-Span-1252"><spanid="MathJax-Span-1253"><spanid="MathJax-Span-1254">y<spanid="MathJax-Span-1255">t<spanid="MathJax-Span-1256">i<spanid="MathJax-Span-1257"><spanid="MathJax-Span-1258"><spanid="MathJax-Span-1259">1<spanid="MathJax-Span-1260">⎞⎠⎟⎟⎟<spanid="MathJax-Span-1261">=<spanid="MathJax-Span-1262"><spanid="MathJax-Span-1263">(<spanid="MathJax-Span-1264"><spanid="MathJax-Span-1265"><spanid="MathJax-Span-1266"><spanid="MathJax-Span-1267">cos<spanid="MathJax-Span-1268"><spanid="MathJax-Span-1269">(<spanid="MathJax-Span-1270">α<spanid="MathJax-Span-1271">)<spanid="MathJax-Span-1272"><spanid="MathJax-Span-1273">x<spanid="MathJax-Span-1274">t<spanid="MathJax-Span-1275">i<spanid="MathJax-Span-1276">+<spanid="MathJax-Span-1277">sin<spanid="MathJax-Span-1278"><spanid="MathJax-Span-1279">(<spanid="MathJax-Span-1280">α<spanid="MathJax-Span-1281">)<spanid="MathJax-Span-1282"><spanid="MathJax-Span-1283">y<spanid="MathJax-Span-1284">t<spanid="MathJax-Span-1285">i<spanid="MathJax-Span-1286"><spanid="MathJax-Span-1287"><spanid="MathJax-Span-1288">−<spanid="MathJax-Span-1289">sin<spanid="MathJax-Span-1290"><spanid="MathJax-Span-1291">(<spanid="MathJax-Span-1292">α<spanid="MathJax-Span-1293">)<spanid="MathJax-Span-1294"><spanid="MathJax-Span-1295">x<spanid="MathJax-Span-1296">t<spanid="MathJax-Span-1297">i<spanid="MathJax-Span-1298">+<spanid="MathJax-Span-1299">cos<spanid="MathJax-Span-1300"><spanid="MathJax-Span-1301">(<spanid="MathJax-Span-1302">α<spanid="MathJax-Span-1303">)<spanid="MathJax-Span-1304"><spanid="MathJax-Span-1305">y<spanid="MathJax-Span-1306">t<spanid="MathJax-Span-1307">i<spanid="MathJax-Span-1308">)<spanrole="presentation"><math xmlns="http://www.w3.org/1998/Math/MathML" display="block"><mrow><mo>[</mo><mtable rowspacing="4pt" columnspacing="1em"><mtr><mtd><mi>cos</mi><mo>⁡</mo><mo stretchy="false">(</mo><mi>α</mi><mo stretchy="false">)</mo></mtd><mtd><mi>sin</mi><mo>⁡</mo><mo stretchy="false">(</mo><mi>α</mi><mo stretchy="false">)</mo></mtd><mtd><mn>0</mn></mtd></mtr><mtr><mtd><mo>−</mo><mi>sin</mi><mo>⁡</mo><mo stretchy="false">(</mo><mi>α</mi><mo stretchy="false">)</mo></mtd><mtd><mi>cos</mi><mo>⁡</mo><mo stretchy="false">(</mo><mi>α</mi><mo stretchy="false">)</mo></mtd><mtd><mn>0</mn></mtd></mtr></mtable><mo>]</mo></mrow><mrow><mo>(</mo><mtable rowspacing="4pt" columnspacing="1em"><mtr><mtd><msubsup><mi>x</mi><mi>i</mi><mi>t</mi></msubsup></mtd></mtr><mtr><mtd><msubsup><mi>y</mi><mi>i</mi><mi>t</mi></msubsup></mtd></mtr><mtr><mtd><mn>1</mn></mtd></mtr></mtable><mo>)</mo></mrow><mo>=</mo><mrow><mo>(</mo><mtable rowspacing="4pt" columnspacing="1em"><mtr><mtd><mi>cos</mi><mo>⁡</mo><mo stretchy="false">(</mo><mi>α</mi><mo stretchy="false">)</mo><msubsup><mi>x</mi><mi>i</mi><mi>t</mi></msubsup><mo>+</mo><mi>sin</mi><mo>⁡</mo><mo stretchy="false">(</mo><mi>α</mi><mo stretchy="false">)</mo><msubsup><mi>y</mi><mi>i</mi><mi>t</mi></msubsup></mtd></mtr><mtr><mtd><mo>−</mo><mi>sin</mi><mo>⁡</mo><mo stretchy="false">(</mo><mi>α</mi><mo stretchy="false">)</mo><msubsup><mi>x</mi><mi>i</mi><mi>t</mi></msubsup><mo>+</mo><mi>cos</mi><mo>⁡</mo><mo stretchy="false">(</mo><mi>α</mi><mo stretchy="false">)</mo><msubsup><mi>y</mi><mi>i</mi><mi>t</mi></msubsup></mtd></mtr></mtable><mo>)</mo></mrow></math></div><script type="math/tex; mode=display" id="MathJax-Element-74">[cos(α)sin(α)0−sin(α)cos(α)0]

(

cos

(α)

+sin

(α)

−sin

(α)

+cos

(α)

)

</script></li> </ul> </div>

关于如何捕获 UIViewAlertForUnsatisfiableConstraints？和如何捕获绿叶蜥的介绍已经告一段落，感谢您的耐心阅读，如果想了解更多关于21、MVSNeRF: Fast Generalizable Radiance Field Reconstruction from Multi-View Stereo、AI-Constraint Satisfaction Problems (CSP)、cocoa-touch – iOS5：有人设法用三个按钮和textfield(UIAlertViewStylePlainTextInput)修复UIAlertView吗？、Deformable ConvNets--Part2: Spatial Transfomer Networks(STN)的相关信息，请在本站寻找。

本文标签：