针对HDU-5834MagicboyBiLuowithhisexcitedtree树形dp好题~这个问题,本篇文章进行了详细的解答,同时本文还将给你拓展C.IlyaAndTheTree树形dp暴力、C
针对HDU - 5834 Magic boy Bi Luo with his excited tree 树形dp 好题~这个问题,本篇文章进行了详细的解答,同时本文还将给你拓展C. Ilya And The Tree 树形dp 暴力、CCPC 2017 哈尔滨 L. Color a Tree && HDU 6241(二分+树形DP)、cf 627 F. Maximum White Subtree【树形dp】、Codeforces 1092F Tree with Maximum Cost(树形DP)等相关知识,希望可以帮助到你。
本文目录一览:- HDU - 5834 Magic boy Bi Luo with his excited tree 树形dp 好题~
- C. Ilya And The Tree 树形dp 暴力
- CCPC 2017 哈尔滨 L. Color a Tree && HDU 6241(二分+树形DP)
- cf 627 F. Maximum White Subtree【树形dp】
- Codeforces 1092F Tree with Maximum Cost(树形DP)

HDU - 5834 Magic boy Bi Luo with his excited tree 树形dp 好题~
题目链接
题意:
给你一棵树,每个结点有个宝藏价值w,每次只能拿一次宝藏,每次经过路径需要花费val值,路径可以来回经过,同时可以多次花费val值,求从i点出发,能拿到的最大权值ans【i】.
思路:
很明显是一个tree dp,但是难点在于怎么去维护,或者说想不全,只能想出一部分。当时也困在如何往父亲走,没法往上dfs.
首先以每个i结点为根节点往下走这个很好维护,我们设dp[i][0]表示从i结点往子树结点走,最后走回i点的最大收益,dp[i][1]表示从i结点往下走,把所有不亏的走完最后不返回i的最大值,dp[i][2]为次大值,id[x]表示dp[i][1]最大值最后是从哪一条边离开的.(为什么要记录从哪条边离开的下面会提到)
我们先来说说怎么求上面这些东西,首先dfs处理好 dp[i][0] .
然后处理dp[i][1],dp[i][2]。 假设当前是父节点x,枚举子节点u(枚举把不亏的都走完从结点u一直往下走了),我们知道dp[x][0]表示从x往下走走回来的,那么有 Now = dp[x][0] - max(0,dp[u][0]-2w)+max(0,dp[u][1]-w)
即如果原来为+ 那肯定走过u了 又回去x了 要减掉,如果dp[u][1]-w不为负就要走获得更大收益.
往下走的处理好了,我们再来处理往上走的,这里就需要用到id[x],我们第二次dfs定义两个参数,up1,up2,表示x的父节点fa,走出去不回来的最大值,up2表示走出去再回来的最大值.
对于一个点x 他的最大收益只取决于两个 max(dp[x][0]+up1,dp[x][1]+up2)
即 max(往下走回来+父节点走出去不回来,往下走不回来+父节点走出去回来)
怎么维护? 对于x和下一步要走的u点,如果id[x] == u,那么就up1就只能用次大值了,否则才可以用最大值. 对于up2就只能看他自己这个分支走没走到,走到就减去否则不减.这个过程是从下往上维护的,所以对于每个x,他的父节点的已经是最优的了.特殊处理一下根节点即可
具体的见代码吧,注释尽量详细一点
#include<bits/stdc++.h> #define pb push_back #define mk make_pair using namespace std; typedef long long ll; const int mod=1e9+7; const int maxn=1e5+10; int n; ll val[maxn]; ll ans[maxn]; vector<pair<ll,ll> > vt[maxn]; ll dp[maxn][4],id[maxn]; /*dp[i][0]从i往下返回i的最大值. dp[i][1]从i往下最后不返回i的最大值 dp[i][2]从i往下最后不返回i的次大值 id[i]表示从i往下最后不返回i的最大值,最后是从哪条边离开的 */ void init() { for(int i = 0;i <= n;++i) { vt[i].clear();//忘记清空,给我一顿RE啊 = = val[i] = 0; ans[i] = 0; dp[i][0] = dp[i][1] = dp[i][2] = id[i] = 0; } return ; } void dfs1(int x,int fa) { dp[x][0] = val[x]; for(int i = 0;i < vt[x].size();++i) { ll u = vt[x][i].first; ll w = vt[x][i].second; if(u == fa) continue; dfs1(u,x); dp[x][0] += max((ll)0,dp[u][0] - 2*w); //先处理dp[x][0] 走出去回来的最大值 } //处理dp[][1],dp[][2],id[x] id[x] = -1; dp[x][1] = dp[x][2] = val[x]; for(int i = 0; i < vt[x].size();++i) { ll u = vt[x][i].first; ll w = vt[x][i].second; if(u == fa) continue; ll Now = dp[x][0] - max((ll)0,dp[u][0] - 2*w) + max((ll)0,dp[u][1] - w); //dp[x][0]是回来的,要减去dp[u][0]的因为从这支离开都走一次 if(Now > dp[x][1]) { dp[x][2] = dp[x][1]; dp[x][1] = Now; id[x] = i; } else if(dp[x][2] < Now) dp[x][2] = Now; } } void dfs2(int x,int fa,ll up1,ll up2) { // up1 x 的父节点走出去不回来的最大值 // up2 x 的父节点走出去回来的最大值 ans[x] = max(up1+dp[x][0],up2+dp[x][1]); for(int i = 0;i < vt[x].size();++i) { ll u = vt[x][i].first; ll w = vt[x][i].second; if(u == fa) continue; ll down1,down2; //down1 下一步的走出去不回来的最优解 //down2 下一步的走出去回来的最优解 if(id[x] == i)//是最优只能走次优了 down1 = dp[x][2] - max((ll)0,dp[u][0]-2*w); else down1 = dp[x][1] - max((ll)0,dp[u][0]-2*w); down2 = max((ll)0,dp[x][0]-max((ll)0,dp[u][0]-2*w)); //down1 要取两个的最优,因为这两种情况都是走出去不回来. //一个是把x子树都走光,从x的父亲离开,一个是把x父亲能走的走光从x下离开. down1 = max((ll)0,max(up1+down2-w,up2+down1-w)); down2 = max((ll)0,up2+down2-2*w); //down2的最优解等于x的fa的走出去回来的最优,加上x走出去回来的(但是要去掉u) dfs2(u,x,down1,down2); } return ; } int main(){ int _; cin>>_; int ca = 1; while(_--) { init(); scanf("%d",&n); for(int i = 1;i <= n;++i) scanf("%lld",&val[i]); for(int i = 1;i < n;++i) { ll u,v,w; scanf("%lld %lld %lld",&u,&v,&w); vt[u].pb(mk(v,w)); vt[v].pb(mk(u,w)); } dfs1(1,0); dfs2(1,0,0); printf("Case #%d:\n",ca++); for(int i = 1;i <= n;++i) printf("%lld\n",ans[i]); } return 0; }

C. Ilya And The Tree 树形dp 暴力
C. Ilya And The Tree
写法还是比较容易想到,但是这么暴力的写法不是那么的敢写。
就直接枚举了每一个点上面的点的所有的情况,对于这个点不放进去特判一下,然后排序去重提高效率。
注意dp[v]一开始存的是从根节点到这个节点都选的情况,这样才好往后转移。


#include <iostream> #include <cstdio> #include <algorithm> #include <vector> #include <cstring> #define inf 0x3f3f3f3f using namespace std; const int maxn = 4e5 + 10; typedef long long ll; int dp[maxn],head[maxn],cnt = 0,a[maxn]; vector<int>vec[maxn]; struct node { int u,v,nxt; node(int u=0,int v=0,int nxt=0):u(u),v(v),nxt(nxt){} }ex[maxn]; void init() { memset(head,-1,sizeof(head)); cnt = 0; } void add(int u,int v) { ex[cnt] = node(u,head[u]); head[u] = cnt++; ex[cnt] = node(v,u,head[v]); head[v] = cnt++; } int gcd(int a,int b) { return b == 0 ? a : gcd(b,a%b); } void dfs(int u,int pre) { for(int i=head[u];i!=-1;i=ex[i].nxt) { int v = ex[i].v; if (v == pre) continue; dp[v] = gcd(dp[u],a[v]); vec[v].push_back(dp[u]); for(int j=0;j<vec[u].size();j++) vec[v].push_back(gcd(vec[u][j],a[v])); sort(vec[v].begin(),vec[v].end()); vec[v].erase(unique(vec[v].begin(),vec[v].end()),vec[v].end()); dfs(v,u); } } int main() { init(); int n; scanf("%d",&n); for (int i = 1; i <= n; i++) scanf("%d",&a[i]); for(int i=1;i<n;i++) { int u,v; scanf("%d%d",&u,&v); add(u,v); } dp[1] = a[1]; vec[1].push_back(0); dfs(1,-1); for (int i = 1; i <= n; i++) dp[i] = max(dp[i],vec[i].back()); for (int i = 1; i <= n; i++) printf("%d ",dp[i]); return 0; }

CCPC 2017 哈尔滨 L. Color a Tree && HDU 6241(二分+树形DP)
题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=6241
题意:给你一棵有 n 个结点的树,每个结点初始颜色都为白色,有 A 个条件:结点 x_i 的黑色结点数目不少于 y_i 个,同时有 B 个条件,除了结点 x_j 及其子树外至少有 y_j 个结点,求把最少要染成黑色结点的数目使得满足 A + B 个条件。
题解:参考自:https://blog.csdn.net/u013534123/article/details/78523559
#include <iostream>
#include <algorithm>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <string>
#include <cmath>
#include <stack>
#include <queue>
#include <vector>
#include <map>
#include <set>
#include <bitset>
using namespace std;
#define ll long long
#define ull unsigned long long
#define mst(a,b) memset((a),(b),sizeof(a))
#define pii pair<int,int>
#define pII pair<ll,ll>
#define pi acos(-1)
#define pb push_back
const double eps = 1e-6;
const int inf = 0x3f3f3f3f;
const ll INF = 0x3f3f3f3f3f3f3f3f;
const int MAXN = 1e5 + 10;
const int MAXM = 1e6 + 10;
int n;
vector<int>vec[MAXN];
int siz[MAXN],b[MAXN],mn[MAXN],mx[MAXN];
int up[MAXN],down[MAXN];
void init() {
for(int i = 0; i <= n; i++) {
vec[i].clear();
b[i] = mn[i] = 0;
}
}
void getsize(int u,int fa) {
siz[u] = 1;
for(int i = 0; i < vec[u].size(); i++) {
int v = vec[u][i];
if(v == fa) continue;
getsize(v,u);
siz[u] += siz[v];
}
}
bool dfs(int u,int fa) {
int l = 0, r = 1;
for(int i = 0; i < vec[u].size(); i++) {
int v = vec[u][i];
if(v == fa) continue;
if(!dfs(v,u)) return false;
l += down[v], r += up[v];
}
down[u] = max(l, mn[u]), up[u] = min(r, mx[u]);
return down[u] <= up[u];
}
bool check(int x) {
for(int i = 1; i <= n; i++) {
mx[i] = min(x - b[i],siz[i]);
if(mx[i] < 0) return false;
}
return dfs(1,0) && down[1] <= x && x <= up[1];
}
int main() {
#ifdef local
freopen("data.txt", "r", stdin);
#endif
int t;
scanf("%d",&t);
while(t--) {
scanf("%d",&n);
init();
for(int i = 1; i < n; i++) {
int u,v;
scanf("%d%d",&u,&v);
vec[u].pb(v);
vec[v].pb(u);
}
getsize(1,0);
int m;
bool flag = true;
scanf("%d",&m);
while(m--) {
int x,y;
scanf("%d%d",&x,&y);
mn[x] = max(mn[x],y);
if(y > siz[x]) flag = false;
}
scanf("%d",&m);
while(m--) {
int x,y;
scanf("%d%d",&x,&y);
b[x] = max(b[x],y);
if(y > n - siz[x]) flag = false;
}
if(!flag) {
puts("-1");
continue;
}
int l = 0, r = n, ans = -1;
while(l <= r) {
int mid = (l + r) >> 1;
if(check(mid)) ans = mid, r = mid - 1;
else l = mid + 1;
}
printf("%d\n",ans);
}
return 0;
}

cf 627 F. Maximum White Subtree【树形dp】


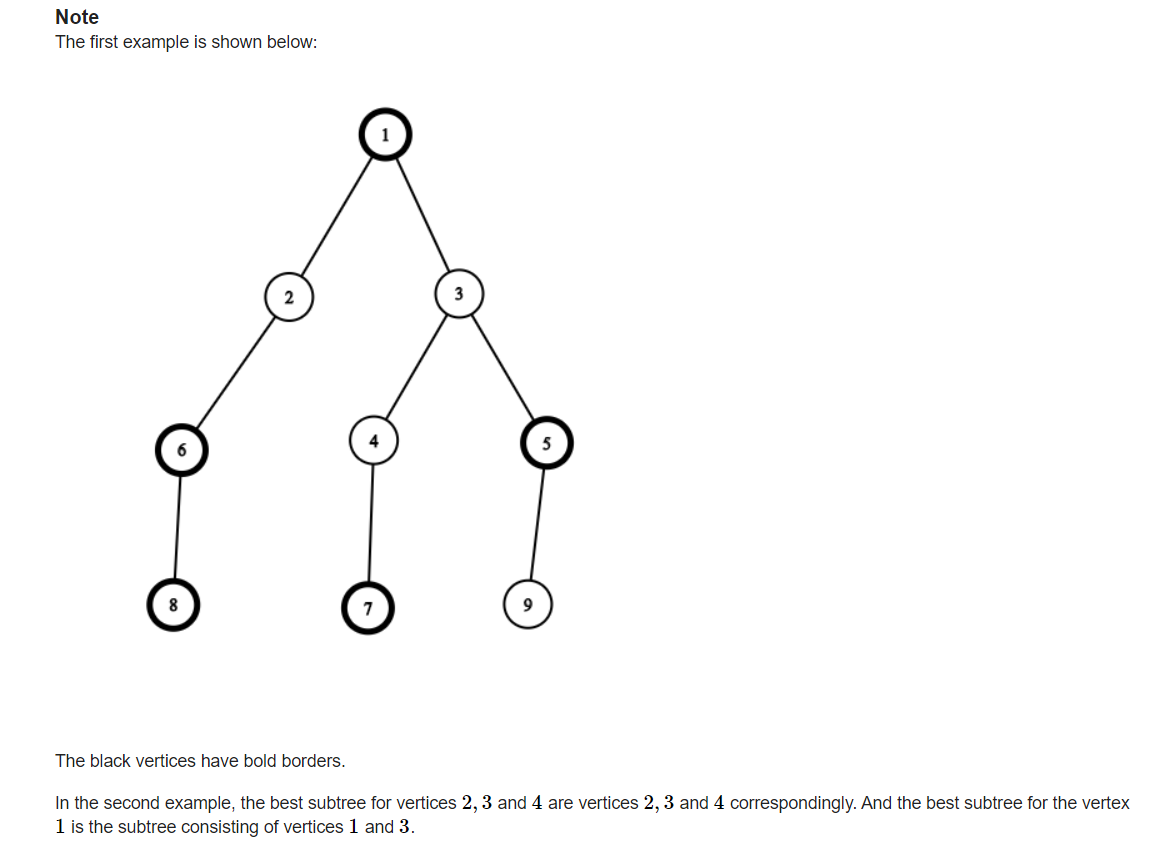
思路
令黑点点权为 -1 , 白点点权为 1,求最大子树点权和。
设 f[i] 为包含 i 点的最大子树点权值,如果当前点的最大点权和 比 当前点父亲的最大点权和小, 则更新当前点。
比较蠢的做法是,分两种情况讨论下,当前点的点权和 大于 或 小于 0 的情况处理是不同的。
如果当前点子树权值 >= 0,且父亲的子树权值更大,应该把父亲点的子树归并到当前点的子树中。
如果当前点子树权值 < 0,且父亲的子树中白的比黑的多,就把父亲点的子树归并到当前点子树上。
CODE
Codeforces 1092F Tree with Maximum Cost(树形DP)
题目链接:Tree with Maximum Cost
题意:给定一棵树,树上每个顶点都有属性值ai,树的边权为1,求$\sum\limits_{i = 1}^{n} dist(i, v) \cdot a_i$,$dist(i, v) $为顶点i到顶点v的距离。该顶点v可以任意选择。
题解:O(n^2)的做法:从每个顶点跑一遍DFS,计算贡献值,并更新答案。(超时)
我们可以先计算出从顶点1跑的答案,发现顶点之间贡献的转移为$ans[u]=ans[fa]+(all-sum[u])-sum[u]$。(all为$\sum\limits_{i = 1}^{n} a_i$)
该顶点的上半部分贡献值增加(all-sum[u]),下半部分贡献值减少(sum[u])。


1 #include <set>
2 #include <map>
3 #include <queue>
4 #include <deque>
5 #include <stack>
6 #include <cmath>
7 #include <cstdio>
8 #include <vector>
9 #include <string>
10 #include <cstring>
11 #include <fstream>
12 #include <iostream>
13 #include <algorithm>
14 using namespace std;
15
16 #define eps 1e-8
17 #define pb push_back
18 #define PI acos(-1.0)
19 #define INF 0x3f3f3f3f
20 #define clr(a,b) memset(a,b,sizeof(a)
21 #define bugc(_) cerr << (#_) << " = " << (_) << endl
22 #define FAST_IO ios::sync_with_stdio(false);cin.tie(NULL);cout.tie(NULL)
23
24 const int N=2e5+10;
25 typedef long long ll;
26 typedef unsigned long long ull;
27 ll a[N],sum[N],res,cnt,ans[N];
28
29 vector <int> E[N];
30
31 void dfs(int u,int fa,ll len){
32 res+=len*a[u];
33 sum[u]=a[u];
34 for(int i=0;i<E[u].size();i++){
35 int v=E[u][i];
36 if(v==fa) continue;
37 dfs(v,u,len+1);
38 sum[u]+=sum[v];
39 }
40 }
41
42 void DFS(int u,int fa){
43 if(fa!=0) ans[u]=ans[fa]+cnt-2*sum[u];
44 for(int i=0;i<E[u].size();i++){
45 int v=E[u][i];
46 if(v==fa) continue;
47 DFS(v,u);
48 }
49 }
50
51 int main(){
52 FAST_IO;
53 int n;
54 cin>>n;
55 for(int i=1;i<=n;i++) cin>>a[i],cnt+=a[i];
56 for(int i=1;i<n;i++){
57 int u,v;
58 cin>>u>>v;
59 E[u].push_back(v);
60 E[v].push_back(u);
61 }
62 dfs(1,0,0);
63 ans[1]=res;
64 DFS(1,0);
65 cout<<*max_element(ans+1,ans+1+n)<<endl;
66 return 0;
67 }
关于HDU - 5834 Magic boy Bi Luo with his excited tree 树形dp 好题~的问题就给大家分享到这里,感谢你花时间阅读本站内容,更多关于C. Ilya And The Tree 树形dp 暴力、CCPC 2017 哈尔滨 L. Color a Tree && HDU 6241(二分+树形DP)、cf 627 F. Maximum White Subtree【树形dp】、Codeforces 1092F Tree with Maximum Cost(树形DP)等相关知识的信息别忘了在本站进行查找喔。
本文标签:



![[转帖]Ubuntu 安装 Wine方法(ubuntu如何安装wine)](https://www.gvkun.com/zb_users/cache/thumbs/4c83df0e2303284d68480d1b1378581d-180-120-1.jpg)

