如果您想了解Swift3andSwift2.3change的知识，那么本篇文章将是您的不二之选。同时我们将深入剖析2019ACM/ICPC全国邀请赛（西安）JAndAndAnd（树DP+贡献计算）、B

如果您想了解Swift 3 and Swift 2.3 change的知识，那么本篇文章将是您的不二之选。同时我们将深入剖析2019 ACM/ICPC 全国邀请赛（西安）J And And And （树 DP + 贡献计算）、Boos And __zp_stoken__ And encrypt And HaHa、camunda and zeebe and activiti and jbpm、CF 979D Kuro and GCD and XOR and SUM（异或 Trie）的各个方面，并给出实际的案例分析，希望能帮助到您！

• Swift 3 and Swift 2.3 change
• 2019 ACM/ICPC 全国邀请赛（西安）J And And And （树 DP + 贡献计算）
• Boos And __zp_stoken__ And encrypt And HaHa
• camunda and zeebe and activiti and jbpm
• CF 979D Kuro and GCD and XOR and SUM（异或 Trie）

Swift 3 and Swift 2.3 change

2019 ACM/ICPC 全国邀请赛（西安）J And And And （树 DP + 贡献计算）

2 
12

0

5 
1 0 
2 0 
3 0 
4 0

35


题意：
给你一颗n个节点的有根树，让你求那个公式的值。

题解：
首先来看如何判定两个节点的路径权值异或起来为0，
我们借助异或的一个这样的性质 x^x=0
那么我们不妨维护出根节点到所有节点的异或值，
如果两个节点x，y，根节点到x的异或值和根节点到y的异或值相等，那么x异或到y的值就一定为0.

接下来我们考虑一对符合条件的节点x，y对答案的贡献。

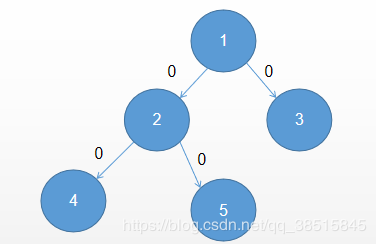
例如这个树中的2和4节点，
我们容易知道，2和4对答案的贡献数量就是4下面那一块（就4这一个节点，）和2右边那一块（2，1，3，5）这四个节点。
那么怎么计算具体的数量呢。

我们把总的贡献数量分为2类来分开求解。
1、计算两个节点在同一条链上。
例如上面说到的2，4就是在同一条链上（这里讲的同一条链上是其中一个节点在和根节点的路径上含有另一个节点。）
那么我们就可以在dfs过程中，在dfs一个节点的子节点之前，把当前节点的贡献加到map里，加的数量用一个变量tmp来维护。
它记录的是该整颗树的节点减去当前节点的子树节点数。那么数量也就是它的子树中的节点如果和它是有效的节点对，
该节点外面可以贡献的节点数量。
当dfs子节点结束后，就返回到之前的数值，对另外一个节点进行dfs，这样可以保证每一次的tmp是针对一个链的。

2、计算不在同一条链上的节点。
同样是dfs，不过这次我们是先dfs，然后更新信息，这样就是一种从下往上更新贡献信息的操作，
因为更新答案是进入dfs就更新的，进入当前节点更新ans的时候，他的子节点还没有加到贡献里，所以就不会重复计算
在同一条立链上的节点，只会计算在不同链上的节点。

本博客参考这个巨巨的博客：https://blog.csdn.net/qq_38515845/article/details/90582561
如果有描述不清楚的地方，可以上这个博客学习。

细节见代码：

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <queue>
#include <stack>
#include <map>
#include <set>
#include <vector>
#include <iomanip>
#define ALL(x) (x).begin(), (x).end()
#define rt return
#define dll(x) scanf("%I64d",&x)
#define xll(x) printf("%I64d\n",x)
#define sz(a) int(a.size())
#define all(a) a.begin(), a.end()
#define rep(i,x,n) for(int i=x;i<n;i++)
#define repd(i,x,n) for(int i=x;i<=n;i++)
#define pii pair<int,int>
#define pll pair<long long ,long long>
#define gbtb ios::sync_with_stdio(false),cin.tie(0),cout.tie(0)
#define MS0(X) memset((X), 0, sizeof((X)))
#define MSC0(X) memset((X), ''\0'', sizeof((X)))
#define pb push_back
#define mp make_pair
#define fi first
#define se second
#define eps 1e-6
#define gg(x) getInt(&x)
#define db(x) cout<<"== [ "<<x<<" ] =="<<endl;
using namespace std;
typedef long long ll;
ll gcd(ll a, ll b) {return b ? gcd(b, a % b) : a;}
ll lcm(ll a, ll b) {return a / gcd(a, b) * b;}
ll powmod(ll a, ll b, ll MOD) {ll ans = 1; while (b) {if (b % 2)ans = ans * a % MOD; a = a * a % MOD; b /= 2;} return ans;}
inline void getInt(int* p);
const int maxn = 100010;
const int inf = 0x3f3f3f3f;
/*** TEMPLATE CODE * * STARTS HERE ***/
int n;
struct node
{
    int next;
    ll x;
};
ll ans = 0ll;
std::vector<node> son[maxn];
const ll mod = 1e9 + 7;
ll num[maxn];
void dfs_num(int x)
{
    // num[x] 代表x的子树的节点个数。
    //
    num[x]++;
    for (auto y : son[x])
    {
        dfs_num(y.next);
        num[x] += num[y.next];
    }
}
map<ll, int> m;
ll tmp = 0ll;
void dfs1(int id, ll s)
{
    // 同一条链
    ans = (ans + 1ll * num[id] * m[s]) % mod;
    for (auto y : son[id])
    {
        tmp = (tmp + 1ll * num[id] - num[y.next]) % mod;
        m[s] = (m[s] + tmp) % mod;
        dfs1(y.next, s ^ y.x);
        m[s] -= tmp;
        m[s] = (m[s] + mod) % mod;
        tmp -= 1ll * num[id] - num[y.next];
        tmp = (tmp + mod) % mod;
    }
}
void dfs2(int id, ll s)
{
    // 不同链
    ans = (ans + 1ll * num[id] * m[s]) % mod;
    for (auto y : son[id])
    {
        dfs2(y.next, s ^ y.x);
    }
    m[s] = (m[s] + num[id]) % mod;
}
int main()
{
    // freopen("D:\\common_text\\code_stream\\in.txt","r",stdin);
    //freopen("D:\\common_text\\code_stream\\out.txt","w",stdout);
    gbtb;
    cin >> n;
    int id; ll x; node temp;
    repd(i, 2, n)
    {
        cin >> id;
        cin >> x;
        temp.x = x;
        temp.next = i;
        son[id].push_back(temp);
    }
    dfs_num(1);
    // db(ans);
    dfs1(1, 0ll);
    m.clear();
    dfs2(1, 0ll);
    cout << (ans + mod) % mod;


    return 0;
}

inline void getInt(int* p) {
    char ch;
    do {
        ch = getchar();
    } while (ch == '' '' || ch == ''\n'');
    if (ch == ''-'') {
        *p = -(getchar() - ''0'');
        while ((ch = getchar()) >= ''0'' && ch <= ''9'') {
            *p = *p * 10 - ch + ''0'';
        }
    }
    else {
        *p = ch - ''0'';
        while ((ch = getchar()) >= ''0'' && ch <= ''9'') {
            *p = *p * 10 + ch - ''0'';
        }
    }
}

Boos And __zp_stoken__ And encrypt And HaHa

该文章主要提供交流学习使用，请勿利用其进行不当行为！

如本篇文章侵犯了贵公司的隐私，请联系我立刻删除！

如因滥用解密技术而产生的风险与本人无关！

已经三个月没写过文章了。

三个月没更新过了。

那就来唠一唠新版的加密吧！

找加密生成的地方：

    省略、、、

    懒得写。。。

    看之前的文章吧。。。

调试的时候，谷歌103浏览器，把我卡死了。。。调着，调着就崩溃了。

我换成了97。。。真爽啊。。。。。。。

因为这个加密是动态的，，动态值，动态js，，

           就连成功率也是动态的。

所以我们要干的就是固定生成出来的结果。

如下：

Math.random = function radom() {
    return 0.5
};
Date.prototype.getTime = function () {
    return 1659509127228
}

当然。。

直接在生成页面运行，是无法固定的。

那怎么才能固定浏览器上的呢。

最简单的办法。

进到加密生成的js中。

运行上述代码。

然后复制m, l,以及  new o 

更改如下。

然后就固定了。

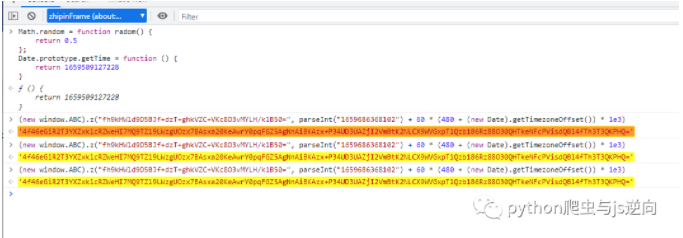
然后复制代码到本地。

开始调试吧。。

你生成出来的，要和浏览器的一模一样，才算可以撒。

当然，少不了proxy

proxy 代理来自如下：

https://developer.mozilla.org/en-US/docs/Web/JavaScript/Reference/Global_Objects/Proxy
 

const docCookies = new Proxy(docCookies, {
  get(target, key) {
    return target[key] || target.getItem(key) || undefined;
  },
  set(target, key, value) {
    if (key in target) { return false; }
    return target.setItem(key, value);
  },
  deleteProperty(target, key) {
    if (!key in target) { return false; }
    return target.removeItem(key);
  },
  ownKeys(target) {
    return target.keys();
  },
  has(target, key) {
    return key in target || target.hasItem(key);
  },
  defineProperty(target, key, descriptor) {
    if (descriptor && ''value'' in descriptor) {
      target.setItem(key, descriptor.value);
    }
    return target;
  },
  getOwnPropertyDescriptor(target, key) {
    const value = target.getItem(key);
    return value ? {
      value,
      writable: true,
      enumerable: true,
      configurable: false,
    } : undefined;
  },
});

温馨提示：

    1. 如果加上代理Proxy。可以解决很多环境问题，但是，你加上了Proxy，代码将会走错误的流程。笑死。哈哈哈哈哈

    2. 本地调试代码。no no no，，检测了格式化。

    3. 他不仅检测了格式化，还要确保你有没有删代码。

    4. 他故意写错几个单词，来误导补环境的，可恶，我被误导了，被他装到了。可恶！！！！

    5. 此window非彼window；

    6. 回到第一条，不会真的以为他检测了什么东西，就要用什么东西吧，不会真的以为没有检测的东西，他就不用了吧？？？

    7. Selenium yyds，我已经报班了，你还在等什么。

当然，长度为145.

你生成的和浏览器生成的为true哦。

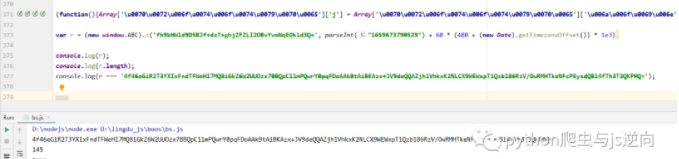
当然，少不了测试。

当然，  记得关注公众号！！！

camunda and zeebe and activiti and jbpm

OSC 请你来轰趴啦！1028 苏州源创会，一起寻宝 AI 时代

jbpm > activiti > camunda >zeebe 

camunda 服务化了 activiti

camunda 子项目 zeebe 

总结：工作流通过 bpmn 文件定义流程，然后通过 api 调用触发节点事件，工作流引擎封装相关公共事情，管理流程状态，流转记录日志。等。触发流程返回工作流流程 ID。绑定业务记录。通过流程 ID 查询工作流引擎的状态，流转记录等！

https://github.com/flowing/flowing-retail

https://github.com/zeebe-io/zeebe-simple-monitor

https://github.com/camunda/camunda-bpm-platform

https://github.com/camunda/camunda-bpm-spring-boot-starter

https://github.com/camunda/camunda-bpm-examples

CF 979D Kuro and GCD and XOR and SUM（异或 Trie）

CF 979D Kuro and GCD and XOR and SUM（异或 Trie）

给出q(<=1e5)个操作。操作分两种，一种是插入一个数u(<=1e5)，另一种是给出三个数x,k,s(<=1e5)，求当前所有u中满足，k|u，x+u<=s，且$x\oplus u$最大的u。

做法好神啊。关于异或的问题有一种常见做法，就是利用01trie来查找在一堆数里面，哪个数与x的异或值最大。这道题就是这个思路。如果去掉k必须整除v这个条件，那么就转化成了上一个问题（只不过有最大值的限制，怎么解决具体看代码）。

这道题的做法非常神奇。我们建1e5个Trie，第i个Trie中插入值为i的倍数的数。这样，查询x,k,s时，只要查询第k个Trie即可，因为里面的数一定满足k|v。插入时要遍历u的所有因数si，然后将u插入第si个Trie。

注意，异或运算是在尾部对齐的，但是要在Trie上贪心，所以必须在插入和查询的数前补零，使他们长度相同。

分析一波复杂度：

• 预处理：我们需要预处理出u的因数。u的最大值为Max=1e5。用类似筛法的方法，时间复杂度是$O(Max(1+\frac{1}{2}+\frac{1}{3}...+\frac{1}{Max}))=O(MaxInMax)$。
• 查询：就是Trie上的查询，总时间复杂度为$O(qlog_2Max)$。
• 插入：一个数最多只有$log_2(Max)$个因数（$2*10^9$内因数最多的数之一是1837836000，有1536个因数），所以总的时间复杂度为$O(qlog^2_2(Max))$。
• 空间复杂度：最多插入$qlog_2(Max)$个数，因此空间复杂度为$qlog_2^2(Max)$。

果然只能膜拜膜拜。

#include <cstdio> 
#include <vector>
using namespace std;

const int maxnum=1e5+5, maxq=1e5+5, maxn=maxq*17*17, INF=1e9;
//maxnum指插入的数的最大值  maxq指查询的最多数目 
//maxn指结点的最多数目(=maxq*插入几个trie*插入数的二进制长度)
int s[maxn][2], minm[maxn], v[maxn], tot;
int q, root[maxnum], use[maxnum];
vector<int> div[maxnum];

void init(){
	for (int i=1; i<maxnum; ++i)
		for (int j=i; j<maxnum; j+=i)
			div[j].push_back(i);
}

//把x插到对应的trie里，注意维护子树中的最小数  l:处理到从左到右第几位 
void insert(int &now, int x, int l){
	if (!now){ now=++tot; minm[now]=INF; }
	minm[now]=min(minm[now], x);
	if (l==-1){ v[now]+=x; return; }
	if ((x>>l)&1) insert(s[now][1], x, l-1);
	else insert(s[now][0], x, l-1);
}

//要找到v<=lim，并且x^v尽量大（贪心）。函数返回v 
//注意由于没有删除操作，路径底下一定有点。 
int query(int now, int x, int lim, int l){  //l:第几位 
	if (l==-1) return v[now];
	int s0=s[now][0], s1=s[now][1];
	if (!s0||minm[s0]>lim) return query(s[now][1], x, lim, l-1);
	if (!s1||minm[s1]>lim) return query(s[now][0], x, lim, l-1);
	if ((x>>l)&1) return query(s[now][0], x, lim, l-1);
	else return query(s[now][1], x, lim, l-1);
}

int main(){
	init();
	scanf("%d", &q); int op, x, k, s;
	for (int i=0; i<q; ++i){
		scanf("%d", &op);
		if (op==1){
			scanf("%d", &x); 
			if (use[x]) continue; use[x]=1;
			for (int j=0; j<div[x].size(); ++j)
				insert(root[div[x][j]], x, 18);
		} else {
			scanf("%d%d%d", &x, &k, &s);
			if (x%k||!minm[root[k]]||minm[root[k]]+x>s) puts("-1");  //注意可能没有一个数 
			else printf("%d\n", query(root[k], x, s-x, 18));  //保证一定有解 
		}
	}
	return 0;
}

关于Swift 3 and Swift 2.3 change的问题我们已经讲解完毕，感谢您的阅读，如果还想了解更多关于2019 ACM/ICPC 全国邀请赛（西安）J And And And （树 DP + 贡献计算）、Boos And __zp_stoken__ And encrypt And HaHa、camunda and zeebe and activiti and jbpm、CF 979D Kuro and GCD and XOR and SUM（异或 Trie）等相关内容，可以在本站寻找。