1 func sqrt1(_ x: Float) -> Float {
 2     //判断x是否为0
 3     if x == 0 {return 0}
 4     let high:Float = Float(x)
 5     let mid:Float = high/2
 6     var y:Float = (mid>1) ? mid : 1
 7     while(true)
 8     {
 9         let dy:Float = (y * y + high) / Float(y)/2
10         //处理float类型的取绝对值fabsf(float i)
11         if fabsf(y - dy) <= 0.00000001
12         {
13             return dy
14         }
15         else
16         {
17             y = dy
18         }
19     }
20 }

(2)、平方根函数：方法2 

 1 func sqrt2(_ x:Float) -> Float
 2 {
 3     var y:Float
 4     var delta:Float
 5     var maxError:Float
 6     if x <= 0 {return 0}
 7     // initial guess
 8     y = x / 2
 9     // refine
10     maxError = x * 0.00000001
11     repeat {
12         delta = ( y * y ) - x
13         y -= delta / ( 2 * y )
14     } while ( delta > maxError || delta < -maxError )
15     return y
16 }

(3)、快速反向平方根：方法1-使用memcpy()

注意开头的导入：import Foundation。

invSqrt(x)比1.0/sqrt(x)快速增加了约40％，

最大相对误差低于0.176％ 

 1 func invSqrt1(_ x: Float) -> Float {
 2     let halfx = 0.5 * x
 3     var y = x
 4     var i : Int32 = 0
 5     memcpy(&i, &y, 4)
 6     i = 0x5f3759df - (i >> 1)
 7     memcpy(&y, &i, 4)
 8     y = y * (1.5 - (halfx * y * y))
 9     return y
10 }

(4)、快速反向平方根：方法2-bitPattern()

从Swift3开始，memcpy()可以用bitPattern:方法替换Float相应的构造函数UInt32:

1 func invSqrt2(_ x: Float) -> Float {
2     let halfx = 0.5 * x
3     var i = x.bitPattern
4     i = 0x5f3759df - (i >> 1)
5     var y = Float(bitPattern: i)
6     y = y * (1.5 - (halfx * y * y))
7     return y
8 }

综合(1)~(4)测试： 

 1 let x:Float = 10.0
 2 let ans1:Float = sqrt1(x)
 3 let ans2:Float = sqrt2(x)
 4 let ans3:Float =  invSqrt1(x)
 5 let ans4:Float =  invSqrt2(x)
 6 print(1/ans1)
 7 //Print 0.31622776
 8 print(1/ans2)
 9 //Print 0.31622776
10 print(ans3)
11 //Print 0.31568578
12 print(ans4)
13 //Print 0.31568578

有趣事情是常量0x5f3759df：它来自哪里？为什么代码有效？

快速逆平方根：有时被称为快速InvSqrt()或由十六进制常数0x5F3759DF的估计¹⁄_√x算法的倒数（或乘法逆）的的平方根的32位的浮点数X在IEEE 754浮点格式。此操作用于数字信号处理以标准化矢量，即将其缩放为长度1.例如，计算机图形程序使用反平方根来计算入射角和反射对照明和阴影。

       该算法接受32位浮点数作为输入，并存储一半的值供以后使用。然后，处理代表浮点数作为一个32位的整数的比特，一个逻辑移位一个位权执行，并且结果从减去幻数 0X 5F3759DF，这是一个近似的浮点表示√2¹²⁷。这导致输入的平方根的第一近似。再次将这些位作为浮点数处理，它运行牛顿方法的一次迭代，产生更精确的近似。

一个有效例子：作为一个例子，数x = 0.15625可用于计算1⁄√x ≈ 2.52982.。该算法的第一步如下所示： 

1 0011_1110_0010_0000_0000_0000_0000_0000  Bit pattern of both x and i
2 0001_1111_0001_0000_0000_0000_0000_0000  Shift right one position: (i >> 1)
3 0101_1111_0011_0111_0101_1001_1101_1111  The magic number 0x5F3759DF
4 0100_0000_0010_0111_0101_1001_1101_1111  The result of 0x5F3759DF - (i >> 1)

使用IEEE 32位表示： 

1 0_01111100_01000000000000000000000  1.25 × 2−3
2 0_00111110_00100000000000000000000  1.125 × 2−65
3 0_10111110_01101110101100111011111  1.432430... × 263
4 0_10000000_01001110101100111011111  1.307430... × 21

将该最后一位模式重新解释为浮点数给出近似值y = 2.61486，其具有大约3.4％的误差。在牛顿方法的一次迭代之后，最终结果是y = 2.52549，误差仅为0.17％。

算法描述：快速反向平方根算法计算¹⁄_√x ，通过执行以下步骤。

(1)、将参数x别名为整数，作为计算log ₂（x）近似值的方法

(2)、使用这种近似计算的近似对数₂（¹ / _√ X）= -1/2日志₂（X）

(3)、别名返回浮点数，作为计算基数2指数近似值的方法

(4)、使用牛顿方法的单次迭代来细化近似。

准确度：下图显示启发式快速反平方根与libstdc提供的平方根直接反转之间差异的图表。（注意两个轴上的对数刻度。）如上所述，近似值令人惊讶地准确。右边的图表描绘了函数的误差（即，通过运行牛顿方法的一次迭代后的近似值的误差），对于从0.01开始的输入，其中标准库给出10.0作为结果，而InvSqrt()给出9.982522，使差值为0.017479，即真值的0.175％。绝对误差仅从此开始下降，而相对误差保持在所有数量级的相同范围内。

Algorithm： GCD、EXGCD、Inverse Element

数论基础

数论是纯数学的一个研究分支，主要研究整数的性质。初等数论包括整除理论、同余理论、连分数理论。这一篇主要记录的是同余相关的基础知识。

取模

取模是一种运算，本质就是带余除法，运算结果就是余数。取模运算结果的符号由被模数（被除数）决定。 $$ 7%4=3;\space7%(-4)=3;\ (-7)%4=-3;\space(-7)%(-4)=-3 $$

取模运算的性质

$$ 设a>b>0，有：\ (a+b)%c=(a%c+b%c)%c\ (a-b)%c=(a%c-b%c+c)%c \ (a\times b)%c=(a%c\times b%c)%c $$

例题1

$$ 给定两个非负整数a，b和正整数n，计算f(a^b)%n。\ 其中，f(0)=f(1)=1,且对于\forall i>0，f(i+2)=f(i+1)+f(i)\ (0\le a,b\le 2^{64},1\le n\le 1000) $$

找规律，对于mod n来说，最多n²项就会出现重复，找出重复项即可得到循环周期，然后找对应的项即可。

例题2：hdu 1212

题意是给一个位数不超过1,000的正整数A和一个大小不超过100,000的正整数B，求A%B。

这里只需要用到上面的两条性质，把A截断，从高到低模拟做除法即可。

#include <iostream>
string s; int mod, ans;
int main() {
    while(std::cin >> str >> mod) {
        ans = 0;
        for(int i = 0; s[i]; i++) ans = (ans * 10 + (s[i] - ''0'')) % mod;
        std::cout << ans << std::endl;
    }
    return 0;
}

GCD

GCD即Greatest Common Divisor，最大公约数。最大公约数即能同时整除给定两个整数的最大正整数。特殊地：gcd（a，0）=a。求解最大公约数通常使用辗转相除法。下面是辗转相除法的代码实现：

typedef long long LL;
LL gcd(LL a, LL b) {
    return b ? gcd(b, a % b) : a;
}

辗转相除法得到的余数序列增长速度比斐波那契数列更快，已知斐波那契的增长是指数级别，则辗转相除法的复杂度是对数级别。

辗转相除法的证明：

1.设两个数a、b（a＞b），他们的最大公约数为gcd（a，b），r = a % b，k = （a - a % b）/ b，那么证明辗转相除法，即是要证明：gcd（a，b）=gcd（b，r）。首先我们令c = gcd（a，b），那么肯定存在互质的整数m，n，使得a = mc，b = nc。那么有r = a - kb = mc - knc = (m - kn)c，根据这条式子，c也是r的因数。回过头看，如果能证明m-kn和n互质，那么就可以说明c=gcd（（m-kn）c，nc）=gcd（b，r），所以把问题再次转化为：求证m-kn和n互质。

2.反证法证明m-kn和n互质：假设m-kn和n不互质，用数学语言描述为：假设存在整数x，y，d，其中d＞1，使得m-kn=xd，n=yd。那么有m=kn+xd=kyd+xd=(ky+x)d，从而a=mc=(ky+x)cd，b=nc=ycd，则gcd（a，b）=cd≠c，与前设矛盾。故m-kn和n互质得证，也就证明了gcd（a，b）=gcd（b，r）。

唯一分解定理

对于任意大于2的正整数X，它总能写成如下形式： $$ X=p_1^{a_1}\times p_2^{a_2} \times ......\times p_k^{a_k}，其中p是各不相同的质数 $$ 即质因数分解。且这个分解唯一。

LCM

LCM即Least Common Multiple，最小公倍数。

$$ \begin{align} &根据唯一分解定理，对于给定的a，b：\ &a=p_1^{a_1}\times p_2^{a_2} \times......\times p_k^{a_k}\ &b=p_1^{b_1}\times p_2^{b_2} \times......\times p_k^{b_k}\ &那么：\ &gcd(a,b)=p_1^{min(a_1,b_1)}\times p_2^{min(a_2,b_2)}\times ......p_1^{min(a_k,b_k)}\ &lcm(a,b)=p_1^{max(a_1,b_1)}\times p_2^{max(a_2,b_2)}\times ......p_1^{max(a_k,b_k)}\ &因此，gcd(a,b)\times lcm(a,b)=a\times b \end{align} $$

LL lcm(LL a, LL b) {
    return a / gcd(a, b) * b;
}

例题：hdu1788

题意是求最小的正整数N，满足除以每一个给定的数Mi，其结果均为Mi-a。作如下转化： $$ N%M_i\equiv(M_i-a)%M_i\Rightarrow (N+a)%M_i=0（a<M_i<100） $$ 即N是Mi的倍数，那么题意也就是求所有M的最小公倍数，注意数字范围即可。

同余

对于两个不同的数a，b，如果有a % p = b % p（p＞1），那我们就称a和b模p同余，记作： $$ a\equiv b(mod\space p) $$

同余的性质

$$ \begin{aligned} &1.自反性：a\equiv a(mod\space m)\ &2.对称性：a\equiv b(mod\space m)，则b\equiv a(mod\space m)\ &3.传递性：若a\equiv b(mod\space m)，b\equiv c(mod\space m)，则a\equiv c(mod\space m)\ &4.线性运算：若a\equiv b(mod\space m)，c\equiv d(mod\space m)\ &\space\space\space则：a\pm c\equiv b\pm d(mod\space m);\space a\times c\equiv b\times d(mod\space m)\ &5.幂运算：若a\equiv b(mod\space m)，那么a^n\equiv b^n(mod\space m)\ &6.若ac\equiv bc(mod\space m)，且c≠0，那么a\equiv b(mod\space {m\over gcd(c,m)})\ &\space\space\space特殊地，若gcd(c,m)=1，则a\equiv b(mod\space m) \end{aligned} $$

EXGCD

贝祖定理（Bezouts Identity）：若设a,b是不全为0的整数，则存在整数x,y，使得ax+by=gcd（a,b），(a,b)代表最大公因数，则设a,b是不全为零的整数，则肯定存在整数x,y，使得ax+by=(a，b)。这个式子称为贝祖等式。

EXtend GCD 即扩展欧几里得算法，它可以用于解关于x，y的贝祖等式。

EXGCD的可行性

当a=0时，ax+by=gcd（a，b）=gcd（0，b）=b，这时可以解出y=1而x为任意。同理可得b=0时，解得x=1而y为任意。当a，b都不为0时： $$ \begin{aligned} &设存在一组解为x_1，y_1，即ax_1+by_1=gcd(a,b)\ &由欧几里得定理：gcd(a,b)=gcd(b,a%b)得：\ &ax_1+by_1=gcd(a,b)=gcd(b,a%b)\ &那么,bx_2+(a%b)y_2=gcd(b,a%b)=ax_1+by_1\ &又a%b=a-a/b\times b\ &\begin {align} 那么，&ax_1+by_1\ =&bx_2+(a-a/b\times b)y_2\ =&bx_2+ay_2-a/bby_2\ =&ay_2+b(x_2-a/by_2) \end{align}\ &故可以得到：x_1=y_2,\space y_1=x_2-a/by_2 \end{aligned} $$ a或b为0即迭代求解的出口，迭代过程用代码表示如下：

typedef long long LL;
// ver 1
// 返回值为gcd（a，b），x和y即求出的特解
LL exgcd(LL a, LL b, LL &x, LL &y) {
    if (b == 0) {
        x = 1; y = 0;
        return a;
    }
    LL ans = exgcd(b, a % b, x, y);
    //这里通过迭代求出了一组解x，y，这组解对应上面推导过程中的x2和y2。
    LL temp = x;
    x = y;
    y = temp - a / b * y;
    return ans;
}

// ver 2
// 在熟悉了推导过程之后，我们可以利用引用的性质得到更为简洁的ver2写法
LL exgcd(LL a, LL b, LL &x, LL &y) {
    if (b == 0) {
        x = 1; y = 0;
        return a;
    }
    LL ans = exgcd(b, a % b, y, x);
    y -= a / b * x;
    return ans;
}

EXGCD的应用

求关于x，y的方程ax+by=c的一组解

这里只需要对贝祖等式稍作变换即可。假设EXGCD求出的方程ax+by=gcd（a，b）的一组解为x1和y1。在方程两边同时乘上一个数m，使得c=m*gcd（a，b），这里也就要求c是gcd（a，b）的倍数，即c%gcd（a，b）=0。这也是方程有解的条件。此时方程为： $$ \begin{align} &ax_1\times m+by_1\times m=gcd(a,b)\times m=c \end{align} $$ 对于ax+by=gcd（a，b），其参数解为： $$ \begin{align} &x=x_1+{b\over gcd(a,b)}\times t,y=y_1-{a\over gcd(a,b)}\times t,t为参数\ &这里选用{b\over gcd(a,b)}和{a\over gcd(a,b)}是为了保证结果均为整数 \end{align} $$ 那么对比方程ax+by=c，可以得到其特解为： $$ \begin{align} &x_0=x_1\times m=x_1\times {c\over gcd(a,b)}\ &y_0=y_1\times m=y_1\times {c\over gcd(a,b)} \end{align} $$ 那么其通解为： $$ \begin{align} &X=x_0+{b\over gcd(a,b)}\times t,Y=y_0-{a\over gcd(a,b)}\times t,t为参数\ &这里选用{b\over gcd(a,b)}和{a\over gcd(a,b)}作为系数是为了确保得到均为整数解。 \end{align} $$ 对于任意一个确定的t，都有一组确定的解与之对应，只需要根据需要找出对应的解即可。

例如求满足ax+by=c的X的最小非负整数解，那么在得到X的通解之后只需调整t，调整过程用伪代码表示为：

S = b / gcd(a, b);
X = (x0 % S + S) % S;
// 由于x0可能是负数，故在模之后还要加上S在取一次模。
// 同理可得Y的最小非负整数解
T = a / gcd(a, b);
Y = (y0 % T + T) % T;

完整的exgcd求解方程ax+by=c的X和Y的最小非负整数解得代码如下：

LL exgcd(LL a, LL b, LL c, LL& x, LL& y) {
    if (b == 0) {
        x = 1; y = 0;
        return a;
    }
    LL ans = exgcd(a, b, c, y, x);
    y -= a / b * x;
    LL S = b / ans, T = a / ans;
    x = (x % S + S) % S;
    y = (y % T + T) % T;
    return ans;
}

求关于x的方程ax≡b（mod m）的最小非负整数解

ax≡b（mod m）即ax%m=b%m，即求ax+my=b%m（取模其实就相当于减去（加上）了若干个模数）。但只有a和m互质时有唯一解，否则无解。转化为ax+my=b（假设b<m）后，套用exgcd即可。

求a关于模数p的乘法逆元

设x是a关于p的乘法逆元，那么有ax≡1（mod p），这是第二个应用的特殊情况，显然也可以通过类似方法求得。

逆元

Inverse Element，逆元，推广了加法中的加法逆元和乘法中的倒数。直观地说，它是一个可以取消另一给定元素运算的元素。a关于模p的逆元存在的条件是gcd（a，p）=1。 $$ \begin{align} &在模p意义下，设A的逆元为A^{-1}，那么有A\times A^{-1}\equiv 1(mod\space p) \end{align} $$ 为什么需要逆元呢？ $$ \begin{align} &在模意义下，{A\over B}%p = {A%p\over B%p}%p并不成立，\ &那么设B在模p意义下的逆元表示为B^{-1}，根据逆元的定义，有{A\over B}=A\times B^{-1}(mod \space p)。 \end{align} $$ 这里，我们把除法转化为乘法，就可以运用取模运算的性质：(a * b) % c = (a % c * b % c) % c，优化算法。

逆元的求法

EXGCD求法

给定模数m，求a的逆元相当于求解关于x的方程ax≡1(mod m)。这个方程可以转化为ax-my=1 。用EXGCD可以求得一组x，y和gcd。检查gcd是否为1（因为EXGCD是把问题转化为求解方程ax-my=gcd（a，m），显然只有gcd（a，m）=1时才能转化），gcd不为1则说明逆元不存在。在能够成功求解的情况下，把解调整x到0~m-1的范围中即可。

费马小定理

在模p为质数的情况下，有费马小定理： $$ a^{p-1}\equiv 1(mod\space p) $$ 那么: $$ a\times a^{p-2}\equiv 1(mod\space p)\ 故a的逆元a^{-1}=a^{p-2} $$ 然后用快速幂求出逆元即可。

拓展：快速幂

// a是底数，b是指数
LL pow(LL a, LL b, LL mod) {
    LL ans = 1;
    while(b) {
        if(b&1) ans = ans * a % mod;
        b >>= 1, a = a * a % mod;
    }
    return ans;
}

拓展：慢速乘，防止快速幂过程中乘法运算爆long long，只需把快速幂中的乘法替换为mul（）即可，一般情况用不上。

// a为因数1，b为因数2
LL mul(LL a, LL b, LL mod) {
    LL ans = 0;
    while(b) {
        if(b&1) ans = (ans + a) % mod;
        b >>= 1, a = (a + a) % mod;
    }
    return ans;
}

欧拉定理

费马小定理其实是欧拉定理的特殊情况。在模数p不为质数时，有： $$ a^{\phi(p)}\equiv 1(其中\phi()是欧拉函数) $$ 同理可以得到： $$ a^{-1}\equiv a^{\phi(p)-1} $$

线性逆元表

有时我们需要快速得出1~p-1的所有逆元，这个时候我们需要一种O（n）的方法，这就是线性逆元表。

首先，1关于任意模p的逆元的逆元都是1。设p = k * i + r（r < i ，1 < i < p），那么有： $$ k\times i + r \equiv0(mod\space p) $$ 利用逆元性质，两边同时乘上i的逆元以及r的逆元，得到： $$ k\times r^{-1}+i^{-1}\equiv 0(mod\space p) $$ 移项得： $$ i^{-1}\equiv-k \times r^{-1}\equiv -⌊{p\over i}⌋\times (p%i)^{-1}(mod\space p) $$ 显然p%i是小于i的，那么我们就可以利用之前的结果在O（1）时间算出单独的逆元。

用代码表示即：

// inv[i]对应i的逆元
LL inv[maxn];
void CalInv() {
	// 0没有逆元，故不初始化
    inv[1] = 1;
    for (int i = 2; i < maxn; i++)
        inv[i] = (mod - mod / i) * inv[mod % i] % mod;
}

利用 $$ (a\times c)% mod = (a%mod\times c%mod)%mod；\ 由a\times a^{-1}\equiv1(mod \space p)得，\ inv_{fac(i)}\equiv inv_{fac(i)}\times (i+1)^{-1}\times (i+1)\equiv inv_{fac(i+1)}\times (i+1)(mod\space p) $$ 我们还可以在线性时间求出1~min(n，p)的阶乘的逆元，代码如下：

LL fac[maxn], inv[maxn];
void CalFacInv() {
    // 0的阶乘是1
    fac[0] = fac[1] = 1;
    for (int i = 2; i < maxn; i++)
        fac[i] = fac[i - 1] * i % mod;
    inv[maxn - 1] = QPow(fac[maxn - 1], mod - 2);
    // 注意边界是≥
    for (int i = maxn - 2; i >= 0; i--)
        inv[i] = inv[i + 1] * (i + 1) % mod;
}

例题：hdu1576

题意即把除法转化为逆元乘法。3种方法的代码：

#include<iostream>
#include<algorithm>
using namespace std;

typedef long long LL;
LL n, B;
const LL mod = 9973;

LL exgcd(LL a, LL b, LL &x, LL &y) {
    if (b == 0) {
        x = 1, y = 0;
        return a;
    }
    LL ans = exgcd(b, a % b, y, x);
    y -= a/b*x;
    return ans;
}

LL QPow(LL x, LL n)
{
    LL res = 1;
    while(n)
    {
        if(n & 1) res = res * x % mod;
        x = x * x % mod;
        n >>= 1;
    }
    return res;
}

LL inv[10000];
void CalInv() {
    inv[1] = 1;
    for (LL i = 2; i < 10000; i++) {
        inv[i] = (mod * mod - mod / i * inv[mod % i]) % mod;
    }
}


int main() {
    CalInv();
    int t;
    cin >> t;
    while (t--) {
        cin >> n >> B;
        // exgcd
        // LL x, y;
        // exgcd(B, mod, x, y);
        // cout << (x + mod) * n % mod << endl;
        
        // QPow
        // cout << QPow(B, mod - 2) * n % mod << endl;
        
        // 逆元打表
        cout << inv[B % mod] * n % mod << endl;
    }
    return 0;
}

原文出处：https://www.cnblogs.com/Li-F/p/11894589.html

Armadillo之求矩阵的逆（inverse）

求一个矩阵的逆（inverse or multiplicative inverse）使用矩阵的.i()方法或用inv()函数

m.i() //返回m的逆

1 若m不是方正的(square)，则函数抛出std::logic_error异常。

2 如果m是奇异的(singular)，则输出的矩阵将被重置，且抛出std::runtime_error异常

inv(m)   //返回m的逆
inv(A,m) //A被设为m的逆

1 若m不是方正的(square)，则函数抛出std::logic_error异常。

2 如果m是奇异的(singular)，则输出的矩阵将被重置，且抛出std::runtime_error异常，同时inv(A,m)返回值将是false

代码：

 mat m = "2,4;3,1;";
 mat m1 = m.i();
 m1.print();
 cout << "-----" << endl;
 mat m2 = inv(m);
 m2.print();
 cout << "-----" << endl;
 mat A;
 inv(A, m);
 A.print();

输出：

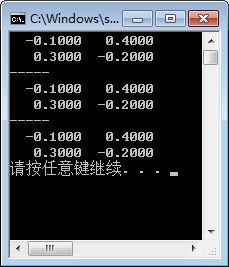
如果矩阵m已经知道是对称的(symmetric)，方阵的(square)，正数的（positive),有限的(definite）则求m的逆使用inv_sympd函数将大大加快运算速度：

A=inv_sympd(m)
inv_sympd(A,m)

以上两种方法运行后A都是m的逆。

1 使用这个函数要启用LAPACK

2 若m不是方正的(square)，则函数抛出std::logic_error异常。

3 现在inv_sympd不检查矩阵m是否是对称，方阵，正数，有限的。

4 如果m是奇异的(singular)，则输出的矩阵将被重置，且抛出std::runtime_error异常，同时inv_sympd(A,m)返回值将是false

Blender, Inverse Kinematics - 即使在减少顶点数量后使用两种方式也无法修复错误“骨热加权”：-

如何解决Blender, Inverse Kinematics - 即使在减少顶点数量后使用两种方式也无法修复错误“骨热加权”：-

在创建骨架并应用自动 IK 后，我做了最后一步，首先选择我的网格然后是骨架，然后执行 Ctrl+P -> ''使用自动权重''。 我得到骨热权重错误（下图），我认为这是由于网格具有许多组件（我还是新手！）。 我尝试通过以下方式减少顶点数量：-

1. 按距离合并，直到形状保持完整的最大距离

2. 应用抽取修饰符并大幅降低比率。
   PIC SHOWING ARMATURE MOVING

   PIC SHOWING THE ERROR

我的电枢移动得很好，但我不能让我的蜘蛛跟着它移动。任何人都知道还有什么其他可能的原因，还是我没有正确修复它？

如果有人可以分析，我会附上我的混合文件吗？ 我一直在关注这个视频：https://www.youtube.com/watch?v=atTKY19u8-o

codeforces 1027 E. Inverse coloring (DP)

E. Inverse Coloring

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

You are given a square board, consisting of $$$n$$$ rows and $$$n$$$ columns. Each tile in it should be colored either white or black.

Let''s call some coloring beautiful if each pair of adjacent rows are either the same or different in every position. The same condition should be held for the columns as well.

Let''s call some coloring suitable if it is beautiful and there is no rectangle of the single color, consisting of at least $$$k$$$ tiles.

Your task is to count the number of suitable colorings of the board of the given size.

Since the answer can be very large, print it modulo $$$998244353$$$.

Input

A single line contains two integers $$$n$$$ and $$$k$$$ ($$$1 \le n \le 500$$$, $$$1 \le k \le n^2$$$) — the number of rows and columns of the board and the maximum number of tiles inside the rectangle of the single color, respectively.

Output

Print a single integer — the number of suitable colorings of the board of the given size modulo $$$998244353$$$.

Examples

Input

1 1

Output

0

Input

2 3

Output

6

Input

49 1808

Output

359087121

Note

Board of size $$$1 \times 1$$$ is either a single black tile or a single white tile. Both of them include a rectangle of a single color, consisting of $$$1$$$ tile.

Here are the beautiful colorings of a board of size $$$2 \times 2$$$ that don''t include rectangles of a single color, consisting of at least $$$3$$$ tiles:

The rest of beautiful colorings of a board of size $$$2 \times 2$$$ are the following:

 

假设现在已经有一个满足条件的矩阵，那么以第一行为基准，所有行要么和它相同，要么相反，如果用0/1分别表示相反/相同的话，从第一行到第n行就可以表示为一个长度为n的0/1序列，同理第一列到第n列也可以表示为长度为n的0/1序列。
当同时知道了行的0/1序列和列的0/1序列，只要再知道矩阵任何一个方格的颜色，就能唯一的表示一个矩阵了。

观察发现，同一种颜色的区域都是矩形，而且它们的大小来自于行和列上连续的0或1。如果把行和列的序列连续的0/1的个数记录下来，比如上面的例子中，行是2,3,3，列是1,2,2,1,2，我们就得到了两个新的序列，并且两个序列的数相乘就是所有色块的面积。
         
自然想到，行中最大的数乘以列中最大的数小于k就是充分必要条件，于是转而分析序列的最大值。
不难发现，序列的最大值可以从1取到n，如果已经知道最大值分别为1,2,3,..n的序列的个数，那么我们只需要让两个序列的最大值两两匹配，遍历所有乘积小于k的情况，就能求出总方案个数。
接下来的问题就是怎么取求最大值分别为1,2,3,..n的序列的个数，也就是说需要解决怎么求最大值为m，和为n的序列的个数。
假设用$$$(n,m)$$$代表最大值为$$$m$$$和为$$$n$$$的任意序列$$$a_1,a_2,...,a_t$$$，注意序列每个数字其实是有颜色的，那么总可以在$$$a_1$$$前面，添加一个颜色相反的数字$$$a_0$$$，如果它不大于$$$m$$$，那么就得到了一个$$$(n+a_0,m)$$$，按照这个思路，如果用$$$dp[n][m]$$$表示序列的个数，可以构造出状态转移方程：
$$$dp[n][m]=dp[n-1][m]+dp[n-2][m]+...+dp[n-m][m]$$$
含义就是$$$(n,m)$$$可以通过在$$$(n-1,m)$$$前面添加$$$1$$$，$$$(n-2,m)$$$前面添加$$$2$$$，...，的方法得到。
注意到一件事，$$$dp[n][m]$$$，当$$$n$$$小于等于$$$m$$$的时候，含义就是和为$$$n$$$的序列，且没有任何限制，那么个数就是$$$2^n$$$
所以状态转移方程就是：
$$$$$$dp[n][m]= \begin{cases} \sum_{i=1}^{m} dp[n-i][m], & {n\gt m} \\[2ex] 2^n, & {n\le m} \end{cases} $$$$$$
进一步发现，对于$$$n>m$$$的部分 $$$$$$\begin{align} dp[n][m] &=dp[n-1][m]+dp[n-2][m]+...+dp[n-m][m]\\ &=dp[n-1][m]+(dp[n-1][m]-dp[n-m-1][m])\\ &=2*dp[n-1][m]-dp[n-m-1][m] \end{align}$$$$$$
所以最终的状态转移方程就是：
$$$$$$dp[n][m]= \begin{cases} 2*dp[n-1][m]-dp[n-m-1][m], & {n\gt m} \\[2ex] 2^n, & {n\le m} \end{cases} $$$$$$

#include<stdio.h>
typedef long long LL;
#define mod 998244353
int dp[502][502];
#define min(a,b) ((a)<(b)?(a):(b))
inline void add(int &a, int b) { a += b; if (a>mod)a -= mod; if (a<0)a += mod; }

void init() {
    int temp;
    dp[1][1] = 1; dp[0][1] = 1;
    for (int t = 2; t <= 500; ++t) {
        dp[t][t] = (dp[t - 1][t - 1] << 1) % mod;
        dp[0][t] = 1;
    }
    for (int k = 1; k <= 500; ++k) {
        for(int n=1;n<=k;++n){
            dp[n][k] = dp[n][n];
        }
        for (int n = k + 1; n <= 500; ++n) {
            dp[n][k] = (2*dp[n-1][k]%mod-dp[n-k-1][k]+mod)%mod;
        }
    }
}

int main() {
    int n, k;
    init();
    scanf("%d %d", &n, &k);
    int ans = 0;
    LL help;
    for (int i = 1; i <= n; ++i) {
        help = dp[n][i] - dp[n][i - 1];
        help = help*(dp[n][min((k - 1) / i,n)]) % mod;
        add(ans, help);
    }
    ans = (ans<<1) % mod;
    printf("%d\n", ans);
}

今天的关于[Swift]快速反向平方根 | Fast inverse square root的分享已经结束，谢谢您的关注，如果想了解更多关于Algorithm： GCD、EXGCD、Inverse Element、Armadillo之求矩阵的逆（inverse）、Blender, Inverse Kinematics - 即使在减少顶点数量后使用两种方式也无法修复错误“骨热加权”：-、codeforces 1027 E. Inverse coloring (DP)的相关知识，请在本站进行查询。