在本文中,我们将为您详细介绍Ubuntu错误—无法从“分数”导入名称“gcd”的相关知识,并且为您解答关于ubuntu无法将grub安装到/dev/sda的疑问,此外,我们还会提供一些关于2017CC
在本文中,我们将为您详细介绍Ubuntu 错误 — 无法从“分数”导入名称“gcd”的相关知识,并且为您解答关于ubuntu无法将grub安装到/dev/sda的疑问,此外,我们还会提供一些关于2017CCPC 杭州 J. Master of GCD【差分标记 / 线段树 / GCD】、CodeForces - 582A GCD Table (map大数操作&gcd)好题、Codeforces Round #554 (Div. 2) C. Neko does Maths(GCD(a,b) = GCD(a,b-a))、CodeForces990G:GCD Counting(树分治+GCD)的有用信息。
本文目录一览:- Ubuntu 错误 — 无法从“分数”导入名称“gcd”(ubuntu无法将grub安装到/dev/sda)
- 2017CCPC 杭州 J. Master of GCD【差分标记 / 线段树 / GCD】
- CodeForces - 582A GCD Table (map大数操作&gcd)好题
- Codeforces Round #554 (Div. 2) C. Neko does Maths(GCD(a,b) = GCD(a,b-a))
- CodeForces990G:GCD Counting(树分治+GCD)
Ubuntu 错误 — 无法从“分数”导入名称“gcd”(ubuntu无法将grub安装到/dev/sda)
如何解决Ubuntu 错误 — 无法从“分数”导入名称“gcd”
我正在使用 Ubuntu 来学习基本的生物信息学。我刚刚使用 conda 下载了 multiqc,但是当我想运行 multiqc 时,它返回: enter image description here
我很天真,不知道如何解决这个问题。任何帮助将不胜感激。谢谢
解决方法
我认为 gcd 在 3.9 中被移到了数学包中。见https://docs.python.org/3/library/fractions.html
在 3.9 版更改:math.gcd() 函数现在用于标准化分子和分母。 math.gcd() 总是返回一个 int 类型。以前,GCD 类型取决于分子和分母。
我建议您使用 3.8 创建一个虚拟环境并尝试一下。有大量关于如何执行此操作的教程。
,正如 Andrew 所说,Python 3.8 可以虚拟安装。然而,我只是要求 Conda 重新安装旧版本的 python (3.8),现在它完美地工作了。
,当您拥有过时版本的 networkx 包时会发生此问题,该包是 MultiQC 依赖项。你可以通过更新这个包来修复它:
conda install networkx=2.5.1
下一版本的 MultiQC (v1.11) 将指定至少需要此版本的 networkx,以确保与 Python 3.9 兼容。
追踪到此问题的 GitHub 问题:https://github.com/ewels/MultiQC/issues/1413

2017CCPC 杭州 J. Master of GCD【差分标记 / 线段树 / GCD】
给你一个 n 个初始元素都为 1 的序列和 m 个询问 q。 询问格式为:l r x (x 为 2or3) 最后求 1~n 所有数的 GCD GCD:把每个数分别分解质因数,再把各数中的全部公有质因数提取出来连乘,所得的积就是这几个数的最大公约数。
#include<cstdio>
#include<string>
#include<cstdlib>
#include<cmath>
#include<iostream>
#include<cstring>
#include<set>
#include<queue>
#include<algorithm>
#include<vector>
#include<map>
#include<cctype>
#include<stack>
#include<sstream>
#include<list>
#include<assert.h>
#include<bitset>
#include<numeric>
#define debug() puts("++++")
#define gcd(a,b) __gcd(a,b)
#define lson l,m,rt<<1
#define rson m+1,r,rt<<1|1
#define fi first
#define se second
#define pb push_back
#define sqr(x) ((x)*(x))
#define ms(a,b) memset(a,b,sizeof(a))
#define sz size()
#define be begin()
#define pu push_up
#define pd push_down
#define cl clear()
#define lowbit(x) -x&x
#define all 1,n,1
#define mod 998244353
#define pi acos(-1.0)
#define rep(i,x,n) for(int i=(x); i<(n); i++)
using namespace std;
typedef long long LL;
typedef unsigned long long ULL;
typedef pair<int,int> P;
const int INF = 1<<30;
const int maxn = 1e5+3;
const double eps = 1e-8;
const int dx[] = {-1,1,0,0,1,1,-1,-1};
const int dy[] = {0,0,1,-1,1,-1,1,-1};
int dir[2]={-1,1};
const int mon[] = {0, 31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31};
const int monn[] = {0, 31, 29, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31};
LL t,n,m;
LL Pow(LL a, LL b)
{
LL res=1;
while(b)
{
if(b&1)
res=(res%mod * a%mod)%mod;
a = a%mod*a%mod;
b>>=1;
}
return res%mod;
}
LL a[maxn],b[maxn];
int main()
{
scanf("%lld",&t);
while(t--)
{
ms(a,0),ms(b,0);
scanf("%lld%lld",&n,&m);
while(m--)
{
LL l,r,x;
scanf("%lld%lld%lld",&l,&r,&x);
if(x==2)
{
a[l]++,a[r+1]--; //差分标记因子含有2的数、区间加维护2or3的操作数
}
else
{
b[l]++,b[r+1]--;
}
}
LL m1=a[1],m2=b[1];
for(int i=2;i<=n;i++)
{
a[i]+=a[i-1]; //前缀和维护序列本身,而序列记录2的操作数即个数,得到具体每个数的操作数
b[i]+=b[i-1];
m1=min(m1,a[i]); //2的最小操作数
m2=min(m2,b[i]);
}
LL ans = (Pow(2,m1)%mod*Pow(3,m2)%mod)%mod;
printf("%lld\n",ans);
}
}
/*
2
5 3
1 3 2
3 5 2
1 5 3
6 3
1 2 2
5 6 2
1 6 2
6 2
【题意】
【类型】
【分析】
【时间复杂度&&优化】
【trick】
【数据】
*/

CodeForces - 582A GCD Table (map大数操作&gcd)好题
| Time Limit: 2000MS | Memory Limit: 262144KB | 64bit IO Format: %I64d & %I64u |
Description
The GCD table G of size n × n for an array of positive integers a of length n is defined by formula
Let us remind you that the greatest common divisor (GCD) of two positive integers x and y is the greatest integer that is divisor of both x and y,it is denoted as
Given all the numbers of the GCD table G,restore array a.
Input
The first line contains number n (1 ≤ n ≤ 500) — the length of array a. The second line contains n2 space-separated numbers — the elements of the GCD table of G for array a.
All the numbers in the table are positive integers,not exceeding 109. Note that the elements are given in an arbitrary order. It is guaranteed that the set of the input data corresponds to some array a.
Output
In the single line print n positive integers — the elements of array a. If there are multiple possible solutions,you are allowed to print any of them.
Sample Input
4 2 1 2 3 4 3 2 6 1 1 2 2 1 2 3 2
4 3 6 2
1 42
42
2 1 1 1 1
1 1
Sample Output
Hint
Source
#include<stdio.h>
#include<string.h>
#include<map>
#include<algorithm>
#include<iostream>
#define N 510
using namespace std;
int gcd(int x,int y)
{
return y==0?x:gcd(y,x%y);
}
map<int,int>m;
int a[N*N],ans[N];
int main()
{
int n,i,j,k;
while(scanf("%d",&n)!=EOF)
{
m.clear();
for(i=1;i<=n*n;i++)
{
scanf("%d",&a[i]);
m[a[i]]++;
}
sort(a+1,a+n*n+1);
int top=0;
for(i=n*n;i>=1;i--)
{
if(!m[a[i]])
continue;
ans[top++]=a[i];//最大的肯定是自身与自身的gcd
m[a[i]]--;
for(j=0;j<top-1;j++)
m[gcd(ans[j],a[i])]-=2;//由表可知,它是对称的,所以 要减去2
}
for(i=0;i<top;i++)
printf("%d ",ans[i]);
printf("\n");
}
return 0;
}

Codeforces Round #554 (Div. 2) C. Neko does Maths(GCD(a,b) = GCD(a,b-a))
传送门
• 题意
给出两个正整数 a,b;
求解 k ,使得 LCM (a+k,b+k) 最小,如果有多个 k 使得 LCM () 最小,输出最小的 k;
• 思路
刚开始推了好半天公式,一顿 xjb 乱操作;
后来,看了一下题解,看到一个引理:
GCD(a,b) = GCD(a,b-a) = GCD(b,b-a);

 简单证明
简单证明假设GCD(a,b) = c; a%c = 0; b%c = 0; 那么(b-a)%c = 0; 这证明了a和(b-a),b和(b-a)有公约数c; 假设GCD(a,b-a)=c'' > c; 那么,a%c'' = 0; (b-a)%c'' = 0; (b-a)%c'' = b%c''-a%c''; 所以 b%c'' = 0; 那么GCD(a,b) = c'' > c,与假设矛盾; GCD(b,b-a)同理; 故命题得证;有了这个引理后,解题思路变得异常清晰;
首先,令 b > a;
将 LCM (a+k,b+k) 转化一下:
情况①,如果 a 与 b-a 不互素,那么 a+1 与 b-a 一定互素;
情况②,a+k = x・(b-a),其中 x・(b-a) 是大于等于 a 的最小的 (b-a) 的倍数;
情况③,枚举 b-a 的约数;
•Code

 View Code
View Code1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 using namespace std; 5 #define ll long long 6 7 ll a,b; 8 9 ll GCD(ll a,ll b) 10 { 11 return a == 0 ? b:GCD(b%a,a); 12 } 13 ll LCM(ll a,ll b) 14 { 15 return a/GCD(a,b)*b; 16 } 17 ll F(ll k) 18 { 19 return (a+k)*(b+k)/GCD(a+k,b+k); 20 } 21 bool isSat(int i,ll k)//判断k是否可以更新为i-a 22 { 23 ll curK=i-a; 24 if(curK < 0 || F(curK) != LCM(a+curK,b+curK)) 25 return false; 26 if(F(curK) < F(k) || F(curK) == F(k) && curK < k) 27 return true; 28 return false; 29 } 30 ll Solve() 31 { 32 if(a > b) 33 swap(a,b); 34 int d=b-a; 35 if(d == 0) 36 return 0; 37 38 ll k=1; 39 for(;GCD(d,a+k) != 1;k++);///情况① 40 for(int i=1;i*i <= d;++i)///情况③ 41 { 42 if(d%i != 0) 43 continue; 44 if(isSat(i,k))///a+k=i 45 k=i-a; 46 if(isSat(d/i,k))///a+k=d/i 47 k=d/i-a; 48 } 49 ///情况②,GCD()为定值,k越小LCM()就越小 50 ll x=(a/d+(a%d == 0 ? 0:1))*d;///a+k=k*d(k*d:>=a的最小的d的倍数) 51 if(isSat(x,k)) 52 k=x-a; 53 54 return k; 55 } 56 int main() 57 { 58 scanf("%lld%lld",&a,&b); 59 printf("%lld\n",Solve()); 60 61 return 0; 62 }
分割线:2019.7.23
・新想法
GCD(b-a , a+k) = f(b-a);
f (b-a) 表示 b-a 的约数;
当 GCD (b-a,a+k) 确定后,k 越小则 LCM (a+k,b+k) 就越小;
假设 GCD (b-a,a+k) = f;
①如果 a 本身就为 f 的倍数,且 GCD (b-a,a) = f;
那么 k = 0 是满足当前条件下,使得 LCM (a+k,b+k) 最小的最优解;
②反之,如果 a 不为 f 的倍数,那么,找到 ≥ a 的最小的 x・f,并判断 GCD (b-a,x・f) ?= f;
1) 如果 GCD (b-a,x・f) = f;
那么 k = x・f-a 是满足当前条件下,使得 LCM (a+k,b+k) 最小的最优解;
2) 如果 GCD (b-a,x・f) ≠ f;
那么 GCD (b-a,(x+1)・f) 一定等于 f;
GCD(b-a,x·f) = GCD(y·f,x·f) = f·GCD(x,y);
判断 GCD (b-a,x・f) ?= f ⇔ 判断 GCD (y,x) ?= 1;
如果 GCD (y,x) ≠ 1,那么一定有 GCD (y,x+1) = 1;
•Code

 View Code
View Code1 #include<bits/stdc++.h> 2 using namespace std; 3 #define GCD(a,b) __gcd(a,b) 4 #define ll long long 5 6 ll a,b; 7 8 ll g(ll k) 9 { 10 return (a+k)/GCD(a+k,b+k)*(b+k); 11 } 12 void update(ll f,ll &k) 13 { 14 ll x=a/f+(a%f != 0);///找到使得x·f ≥ a的最小的x 15 ll y=(b-a)/f; 16 17 if(GCD(x,y) != 1) 18 x++; 19 20 ///判断是否更新k 21 ll cur=x*f-a; 22 if(k == -1 || g(k) > g(cur)) 23 k=cur; 24 else if(g(k) == g(cur)) 25 k=min(k,cur); 26 } 27 ll Solve() 28 { 29 if(a == b) 30 return 0; 31 if(b < a) 32 swap(a,b); 33 34 ll k=-1; 35 36 for(ll i=1;i*i <= b-a;++i) 37 { 38 if((b-a)%i != 0) 39 continue; 40 41 update(i,k); 42 update((b-a)/i,k); 43 } 44 45 return k; 46 } 47 int main() 48 { 49 scanf("%lld%lld",&a,&b); 50 printf("%lld\n",Solve()); 51 52 return 0; 53 }

CodeForces990G:GCD Counting(树分治+GCD)
You are given a tree consisting of nn vertices. A number is written on each vertex; the number on vertex ii is equal to aiai.
Let''s denote the function g(x,y)g(x,y) as the greatest common divisor of the numbers written on the vertices belonging to the simple path from vertex xx to vertex yy(including these two vertices).
For every integer from 11 to 2⋅1052⋅105 you have to count the number of pairs (x,y)(x,y) (1≤x≤y≤n)(1≤x≤y≤n) such that g(x,y)g(x,y) is equal to this number.
Input
The first line contains one integer nn — the number of vertices (1≤n≤2⋅105)(1≤n≤2⋅105).
The second line contains nn integers a1a1, a2a2, ..., anan (1≤ai≤2⋅105)(1≤ai≤2⋅105) — the numbers written on vertices.
Then n−1n−1 lines follow, each containing two integers xx and yy (1≤x,y≤n,x≠y)(1≤x,y≤n,x≠y)denoting an edge connecting vertex xx with vertex yy. It is guaranteed that these edges form a tree.
Output
For every integer ii from 11 to 2⋅1052⋅105 do the following: if there is no pair (x,y)(x,y) such that x≤yx≤y and g(x,y)=ig(x,y)=i, don''t output anything. Otherwise output two integers: iiand the number of aforementioned pairs. You have to consider the values of ii in ascending order.
See the examples for better understanding.
Examples
3
1 2 3
1 2
2 31 4
2 1
3 16
1 2 4 8 16 32
1 6
6 3
3 4
4 2
6 51 6
2 5
4 6
8 1
16 2
32 14
9 16 144 6
1 3
2 3
4 31 1
2 1
3 1
6 2
9 2
16 2
144 1题意:求所有简单路径的GCD,统计数量。
思路:不难想到是分治,问题转化为多个小问题:统计经过某点的路径的GCD,由于GCD具有收敛性,不同GCD的数量级是log级别的,虽然有多个链,但感觉gcd是数量就算不会太多,2333,我猜复杂度不超过O(N*logN*logN*logN)级别吧。所以对于当前子树,每次访问一条链的时候统计这条链和之前所有GCD的gcd。。。。说不清楚,反正一想就会相通的东西。
(具有收敛性的有:GCD,或,且...)
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int maxn=200010;
const int inf=0x7FFFFFFF;
int Laxt[maxn],Next[maxn<<1],To[maxn<<1],cnt,N,sn;
int a[maxn],sz[maxn],son[maxn],vis[maxn],root; ll ans[maxn];
map<int,int>mp,tp;
map<int,int>::iterator it1,it2;
inline void read(int &x) {
x=0; char c=getchar();
while(c>''9''||c<''0'') c=getchar();
while(c<=''9''&&c>=''0'') x=(x<<3)+(x<<1)+c-''0'',c=getchar();
}
void add(int u,int v){
Next[++cnt]=Laxt[u];
Laxt[u]=cnt; To[cnt]=v;
}
void getroot(int u,int fa) //找重心
{
sz[u]=1; son[u]=0;
for(int i=Laxt[u];i;i=Next[i]){
if(To[i]!=fa&&!vis[To[i]]){
getroot(To[i],u);
sz[u]+=sz[To[i]];
son[u]=max(son[u],sz[To[i]]);
}
}
son[u]=max(son[u],sn-son[u]);
if(root==0||son[root]>son[u]) root=u;
}
void getans(int u,int fa,int num) //对于当前链产生的新GCD
{
tp[num]++;
for(int i=Laxt[u];i;i=Next[i]){
if(!vis[To[i]]&&To[i]!=fa){
getans(To[i],u,__gcd(num,a[To[i]]));
}
}
}
void solve(int u) //解决以u为根的子问题
{
mp.clear(); mp[a[u]]++; ans[a[u]]++;
for(int i=Laxt[u];i;i=Next[i])
if(!vis[To[i]]) {
tp.clear(); getans(To[i],u,__gcd(a[u],a[To[i]]));
for(it1=mp.begin();it1!=mp.end();it1++)
for(it2=tp.begin();it2!=tp.end();it2++){
int g=__gcd((*it1).first,(*it2).first);
ans[g]+=(ll)(*it1).second*(*it2).second;
}
for(it2=tp.begin();it2!=tp.end();it2++)
mp[(*it2).first]+=(*it2).second;
}
}
void dfs(int u) //分治
{
vis[u]=1; solve(u);
for(int i=Laxt[u];i;i=Next[i]){
if(vis[To[i]]) continue;
root=0; sn=sz[To[i]];
getroot(To[i],0); dfs(root);
}
}
int main()
{
read(N); int u,v,Max=0;
for(int i=1;i<=N;i++) read(a[i]),Max=max(Max,a[i]);
for(int i=1;i<N;i++) {
read(u);read(v);
add(u,v); add(v,u);
}
root=0; sn=N; getroot(1,0); dfs(root);
for(int i=1;i<=Max;i++) if(ans[i]) printf("%d %I64d\n",i,ans[i]);
return 0;
}
关于Ubuntu 错误 — 无法从“分数”导入名称“gcd”和ubuntu无法将grub安装到/dev/sda的问题就给大家分享到这里,感谢你花时间阅读本站内容,更多关于2017CCPC 杭州 J. Master of GCD【差分标记 / 线段树 / GCD】、CodeForces - 582A GCD Table (map大数操作&gcd)好题、Codeforces Round #554 (Div. 2) C. Neko does Maths(GCD(a,b) = GCD(a,b-a))、CodeForces990G:GCD Counting(树分治+GCD)等相关知识的信息别忘了在本站进行查找喔。
本文标签:


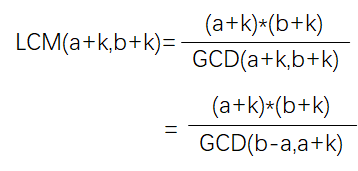
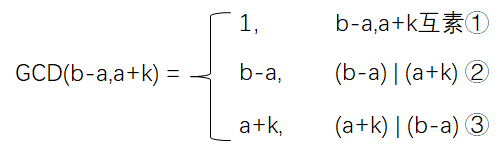


![[转帖]Ubuntu 安装 Wine方法(ubuntu如何安装wine)](https://www.gvkun.com/zb_users/cache/thumbs/4c83df0e2303284d68480d1b1378581d-180-120-1.jpg)

