在这里,我们将给大家分享关于Python混合整数线性规划的知识,让您更了解python混合整数规划的本质,同时也会涉及到如何更有效地C/C++和python混合编程-1、javaweb中java和py
在这里,我们将给大家分享关于Python混合整数线性规划的知识,让您更了解python 混合整数规划的本质,同时也会涉及到如何更有效地C/C++和python混合编程-1、java web中java和python混合使用、Matlab 整数线性规划问题模型代码、MATLAB学习(七)求解优化问题:线性规划 非线性规划 拟合与插值 多目标规划的内容。
本文目录一览:- Python混合整数线性规划(python 混合整数规划)
- C/C++和python混合编程-1
- java web中java和python混合使用
- Matlab 整数线性规划问题模型代码
- MATLAB学习(七)求解优化问题:线性规划 非线性规划 拟合与插值 多目标规划

Python混合整数线性规划(python 混合整数规划)
是否有适用于Python的混合整数线性编程(MILP)求解器?
GLPK python可以解决MILP问题吗?我读到它可以解决混合整数问题。
我是线性编程问题的新手。因此,如果混合整数编程与混合整数线性编程(MILP)不同,我会很困惑,无法真正区分。

C/C++和python混合编程-1
C/C++中或者unity或者cocos2d等中,通常嵌入Lua脚本语言来进行游戏开发。
在这里可以C/C++中嵌入式python脚本来辅助游戏开发。可以采用 boost::python和Python C-API来进行。
step:下载python 2.7 x64,boost 1.6.0 VS2015 安装,并且正确设置python环境变量。
step:新建python脚本 1.py print("Hello, World!")
step:添加boost.python库,编写C++代码:
#include "boost/python.hpp"
int main(int argc, char* argv[])
{
using namespace boost::python::api;
using namespace boost::python;
Py_Initialize();
boost::python::exec_file("1.py");
system("pause");
return 0;
}
F5运行
注:在这里不是标准嵌入式,还需要依托于本机安装的python环境。
官方标准嵌入式文档 https://www.boost.org/doc/libs/1_65_1/libs/python/doc/html/tutorial/tutorial/embedding.html

java web中java和python混合使用
利用java web技术展示python算法处理后的数据
工具/原料
-
myeclipse10
-
pycharm+Anaconda2
方法/步骤
-
首先安装配置好pycharm+Anaconda2
特别的,需要配置好python的环境变量,因为在用java调用python 的时候,需要通过线程调用
-
测试环境变量是否配置成功
在命令窗口输入python,显示如下则说明配置成功
-
将写好的python工程代码放置在Anaconda2的Lib目录下面
这里是Anaconda2安装的目录
例如我安装在D:\adt-bundle-windows-x86-20131030\Anaconda2
我的工程文件是content_recommender_core
那么就放在D:\adt-bundle-windows-x86-20131030\Anaconda2\Lib
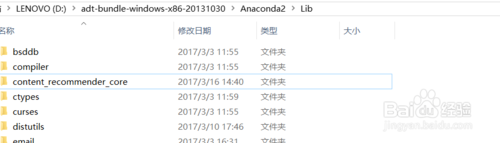
-
现在将写好的python文件放置到java web工程上去,这个文件的存放与java web文件的建立类似,所以可以放置在任何路径下,例如我是放在src目录下
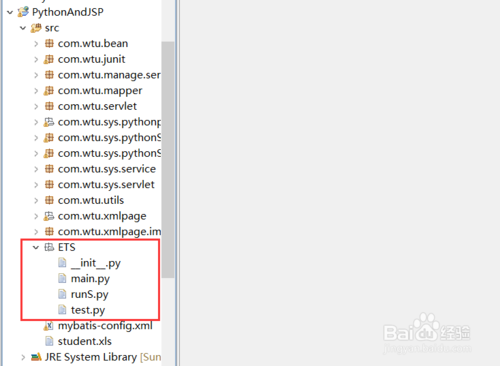
-
放置好所有文件之后,就是到了最关键的时候,那就是需该对应的文件路径
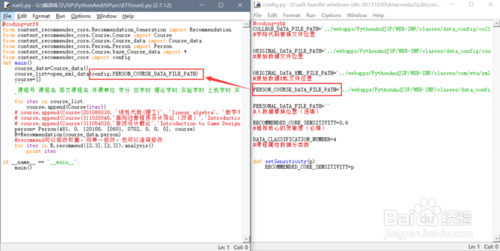
其中最重要的是需该python 代码中的config.py文件的路径
因为工程部署到了tomcat之后,相对的路径就会有些变化,所以需要修改
-
例如python需要读取的文件是在我的tomcat的/webapps/PythonAndJSP/WEB-INF/classes/com/wtu/xmlpage/course.xml,那么config.py文件中的路径设置应该是../webapps/PythonAndJSP/WEB-INF/classes/com/wtu/xmlpage/course.xml

-
为了达到路径的统一化修改,建议使用相对路径,那么在run.py文件中,可以这样设置路径,之后的路径变化,就只要修改config.py文件了
也就是需要引用的文件直接通过变量名引用
-
所有的工作做好之后,就是测试
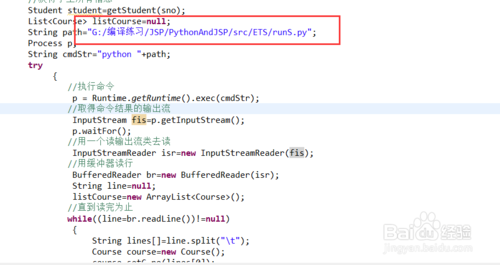
测试的主要代码
String path="G:/编译练习/JSP/PythonAndJSP/src/ETS/runS.py";
Process p;
String cmdStr="python "+path;
try
{
//执行命令
p = Runtime.getRuntime().exec(cmdStr);
//取得命令结果的输出流
InputStream fis=p.getInputStream();
p.waitFor();
//用一个读输出流类去读
InputStreamReader isr=new InputStreamReader(fis);
//用缓冲器读行
BufferedReader br=new BufferedReader(isr);
String line=null;
listCourse=new ArrayList<Course>();
//直到读完为止
while((line=br.readLine())!=null)
{
String lines[]=line.split("\t");
其中读取python执行文件的代码路径只能是本地上存放的文件位置,也就是说不能是tomcat上面的文件
-
9
到这里,所有的工程做完,可以正确运行得到最后的结果了

Matlab 整数线性规划问题模型代码

整数线性规划问题的基本内容
整数线性规划解决的是自变量在一定的线性约束条件下,使得线性目标函数求得最大值或者最小值的问题。其中自变量只能取整数。特别地,当自变量只能取0或者1时,称之为 0-1 整数规划问题。
当目标函数为最小值时,上述问题可以写成如下形式:
$$ \min z=\mathbf{F}^{T}\mathbf{X} $$
$$ \text { s.t. } \left{\begin{array}{l} {\mathbf{A}\mathbf{X} \leqslant \mathbf{B}} \ {\mathbf{A}{\mathrm{eq}} \mathbf{X}=\mathbf{B}{\mathrm{eq}}} \ {\mathbf{LB} \leqslant \mathbf{X} \leqslant \mathbf{UB}} \\mathbf{X} \text{取整数} \end{array}\right. $$
其中
$F$线性目标函数系数向量
$\mathbf{X}$ 为决策变量向量
$\mathbf{A}$ 为线性不等式系数矩阵
$\mathbf{B}$ 为线性不等式右端常数向量
$\mathbf{A}_\mathrm{eq}$ 为线性等式系数矩阵
$\mathbf{B}_\mathrm{eq}$ 为线性等式右端常数向量
$\mathbf{L B}$ 为决策变量下界向量
$\mathbf{U B}$ 为决策变量上界向量
<br/>
Matlab模型代码
调用形式
[X,FVAL,EXITFLAG,OUTPUT,LAMBDA] = intlinprog(F,intcon,A,B,Aeq,Beq,LB,UB) % 统一形式
输入变量
- F为目标函数系数向量
- intcon为整数变量的地址
- A 为不等式约束系数矩阵(注意默认不等式方向为小于等于,若为大于等于,需要将其取相反数)
- B 为不等式右端常数向量(注意默认不等式方向为小于等于,若为大于等于,需要将其取相反数)
- Aeq 为等式约束系数矩阵
- Beq 为等式右端常数向量
- LB 为决策变量下界向量
- UB为决策变量上界向量
在调用时,输入参数不存在时,可以将其输入用 [] 空矩阵表示。
输出变量
- X 为最优解
- FVAL 为最优目标值
- EXITFLAG 为运行结束标志,当等于1时,表示程序收敛于解 X;当等于0时,表示程序运行次数到达最大;当小于0时,说明情况较多
- OUTPUT 为程序迭代次数
- LAMBDA 为解X相关的Largrange乘子和影子价格
<br/>
案例演示
目标函数与约束条件
$$\min z=-3 x_{1}-2 x_{2}-x_{3}$$ $$\text { s. t. }\left{\begin{array}{l}{x_{1}+x_{2}+x_{3} \leq 7} \ {4 x_{1}+2 x_{2}+x_{3}=12} \ {x_{1}, x_{2} \geqslant 0} \ {x_{3}=0\text{ or }1}\end{array}\right.$$
Matlab程序
clc,clear
f = [-3;-2;-1];
intcon = 3; % 整数变量的地址
A = ones(1,3);
B = 7;
Aeq = [4,2,1];
Beq = 12;
LB = zeros(3,1);
UB = [inf;inf;1]; % 只有x(3)取0或者1
[x,fval]= intlinprog(f,intcon,A,B,Aeq,Beq,LB,UB)
运行结果
x =
0
5.5000
1.0000
fval =
-12.0000

MATLAB学习(七)求解优化问题:线性规划 非线性规划 拟合与插值 多目标规划


Minf(x)=-5x1 -4x2 -6x3
x1 -x2 +x3 <=20
3x1 +2x2 +4x3 <=42
3x1 +2x2 <=30
0<=x1,0<=x2,0<=x3
>> c=[-5,-4,-6];
>> A=[1 -1 1
3 2 4
3 2 0];
>> b=[20;42;30];
>> lb=zeros(3,1);
>> [x,fval,exitflag,output,lambda]=linprog(c,A,b,[],[],lb)
Optimization terminated.
x =
0.0000
15.0000
3.0000
fval =
-78.0000
exitflag =
1
output =
iterations: 6
algorithm: ''interior-point-legacy''
cgiterations: 0
message: ''Optimization terminated.''
constrviolation: 0
firstorderopt: 5.8705e-10
lambda =
ineqlin: [3x1 double]
eqlin: [0x1 double]
upper: [3x1 double]
lower: [3x1 double]
>>


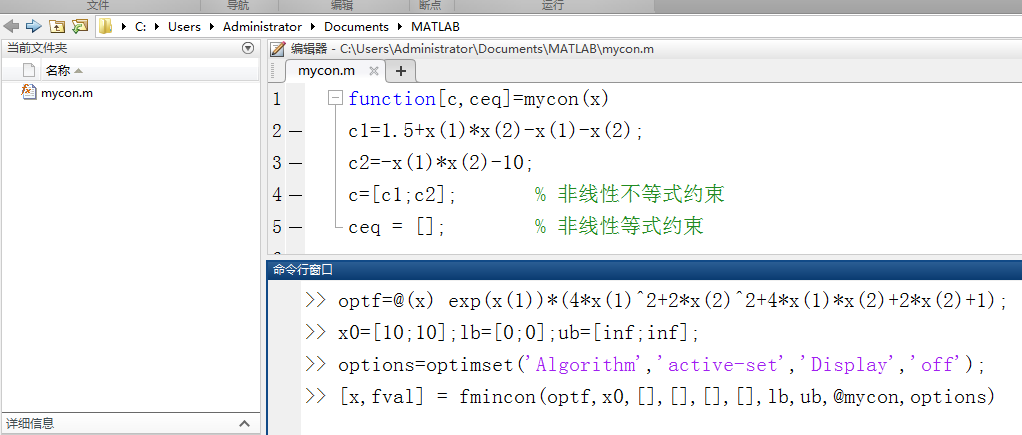
function[c,ceq]=mycon(x)
c1=1.5+x(1)*x(2)-x(1)-x(2);
c2=-x(1)*x(2)-10;
c=[c1;c2]; % 非线性不等式约束
ceq = []; % 非线性等式约束
>> optf=@(x) exp(x(1))*(4*x(1)^2+2*x(2)^2+4*x(1)*x(2)+2*x(2)+1);
>> x0=[10;10];lb=[0;0];ub=[inf;inf];
>> options=optimset(''Algorithm'',''active-set'',''Display'',''off'');
>> [x,fval] = fmincon(optf,x0,[],[],[],[],lb,ub,@mycon,options)
x =
0
1.5000
fval =
8.5000
>>


>> x=0:.1:5;
>> y=sin(x);
>> f=@(b,x) b(1)*cos(b(2)*x+b(3))+b(4);
>> [a,ss]=lsqcurvefit(f,[1,1,1,1],x,y)
Local minimum found.
Optimization completed because the size of the gradient is less than
the default value of the function tolerance.
<stopping criteria details>
a =
-1.0000 1.0000 1.5708 -0.0000
ss =
8.7594e-29
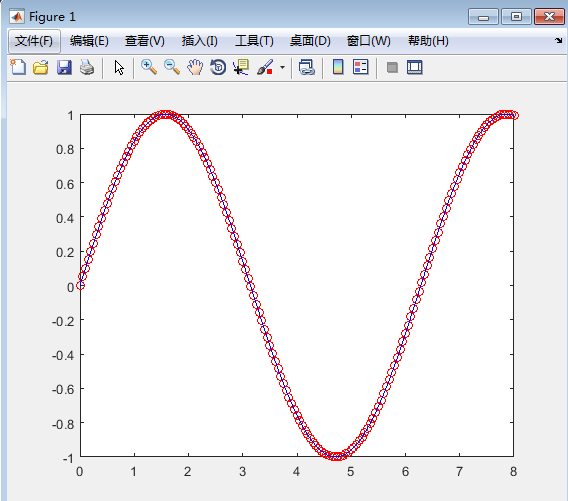
>> xf=0:0.05:8;
yfit=f(a,xf);
plot(xf,sin(xf),''ro'',xf,yfit,''b-'')

>> zf=@(a,x) a(1)*x(:,1).^2+a(2)*x(:,2).^2+a(3) %构造拟合函数类型
zf =
@(a,x)a(1)*x(:,1).^2+a(2)*x(:,2).^2+a(3)
>> [X0,Y0]=meshgrid(-2:.2:2);
x0=X0(:);y0=Y0(:);
z0=zf([1,1,-1],[x0,y0]);
>> %用上面的点去拟合估计曲面函数中的参数a:
>> [b,re]=nlinfit([x0,y0],z0,zf,[0,0,0]);
b %显示b,发现恰好是1、1、-1
b =
1.0000 1.0000 -1.0000

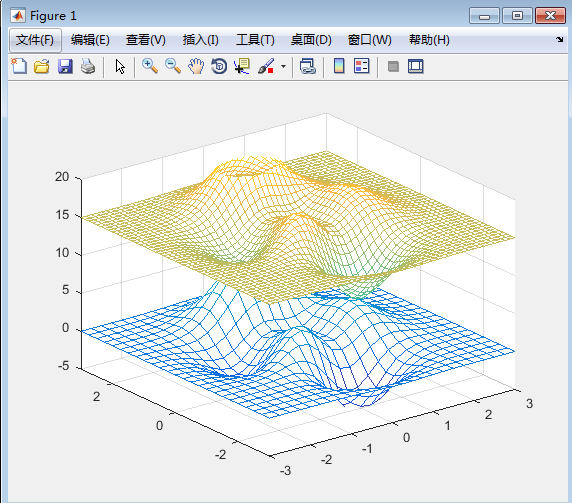
>> [X,Y] = meshgrid(-3:.25:3);Z = peaks(X,Y);
[XI,YI] = meshgrid(-3:.125:3);
ZI = interp2(X,Y,Z,XI,YI);
mesh(X,Y,Z), hold, mesh(XI,YI,ZI+15), hold off
axis([-3 3 -3 3 -5 20])
已锁定最新绘图
>>

我们今天的关于Python混合整数线性规划和python 混合整数规划的分享已经告一段落,感谢您的关注,如果您想了解更多关于C/C++和python混合编程-1、java web中java和python混合使用、Matlab 整数线性规划问题模型代码、MATLAB学习(七)求解优化问题:线性规划 非线性规划 拟合与插值 多目标规划的相关信息,请在本站查询。
本文标签:



![[转帖]Ubuntu 安装 Wine方法(ubuntu如何安装wine)](https://www.gvkun.com/zb_users/cache/thumbs/4c83df0e2303284d68480d1b1378581d-180-120-1.jpg)

